Chain of Thought Reasoning

Graham Neubig

Carnegie Mellon University Language Technologies Institute

Motivation: Complex Reasoning Tasks

  • “What is the fastest an H100 GPU could possibly generate 100 tokens from LLaMA 3 8B?”
  • Knowledge Recall: What are the FLOPS of an H100 and size of LLaMA 3 8B?
  • Multi-step Reasoning: How can I set up calculation to calculate FLOPS for 100 tokens?
  • Computation: Perform the actual computation (alternative - run a program)

The Fundamental Challenge

Not All Problems Are Created Equal:

  • Simple: “What is 2 + 3?”
  • Medium: “If a train travels 60 mph for 2.5 hours, how far does it go?”
  • Complex: “A company’s revenue grew 15% annually for 3 years, then declined 8% in year 4. If final revenue was $2.3M, what was the initial revenue?”

Key Insight: Harder problems should use more computational resources

Question: How can we allocate computation based on problem difficulty?

Adaptive Computation Time (Graves, 2016)

Core Idea: Dynamically adjust computational effort based on input complexity

  • RNNs learn how many computational steps to take
  • Halting mechanism: Learned function \(p_n = \sigma(W_p s_n + b_p)\) predicts when to stop
  • Training: End-to-end with additional “ponder cost” \(\mathcal{L}_{ponder} = \sum_n p_n\) to encourage efficiency

Reference: Adaptive Computation Time for Recurrent Neural Networks - See Figure 1

Chain of Thought (Wei et al., 2022)

Generate intermediate reasoning steps before producing the final answer

Formal Definition:

  • Input: \(x\) (problem statement)
  • Chain of Thought: \(z\) (intermediate reasoning steps)
  • Output: \(y\) (final answer)
  • Goal: \(P(y \mid x) \rightarrow \sum_z P(z, y \mid x)\)

Advantages:

  • Extra tokens provide adaptive computation time
  • If the chain of thought is faithful, allows for verification of reasoning

Illustration of CoT

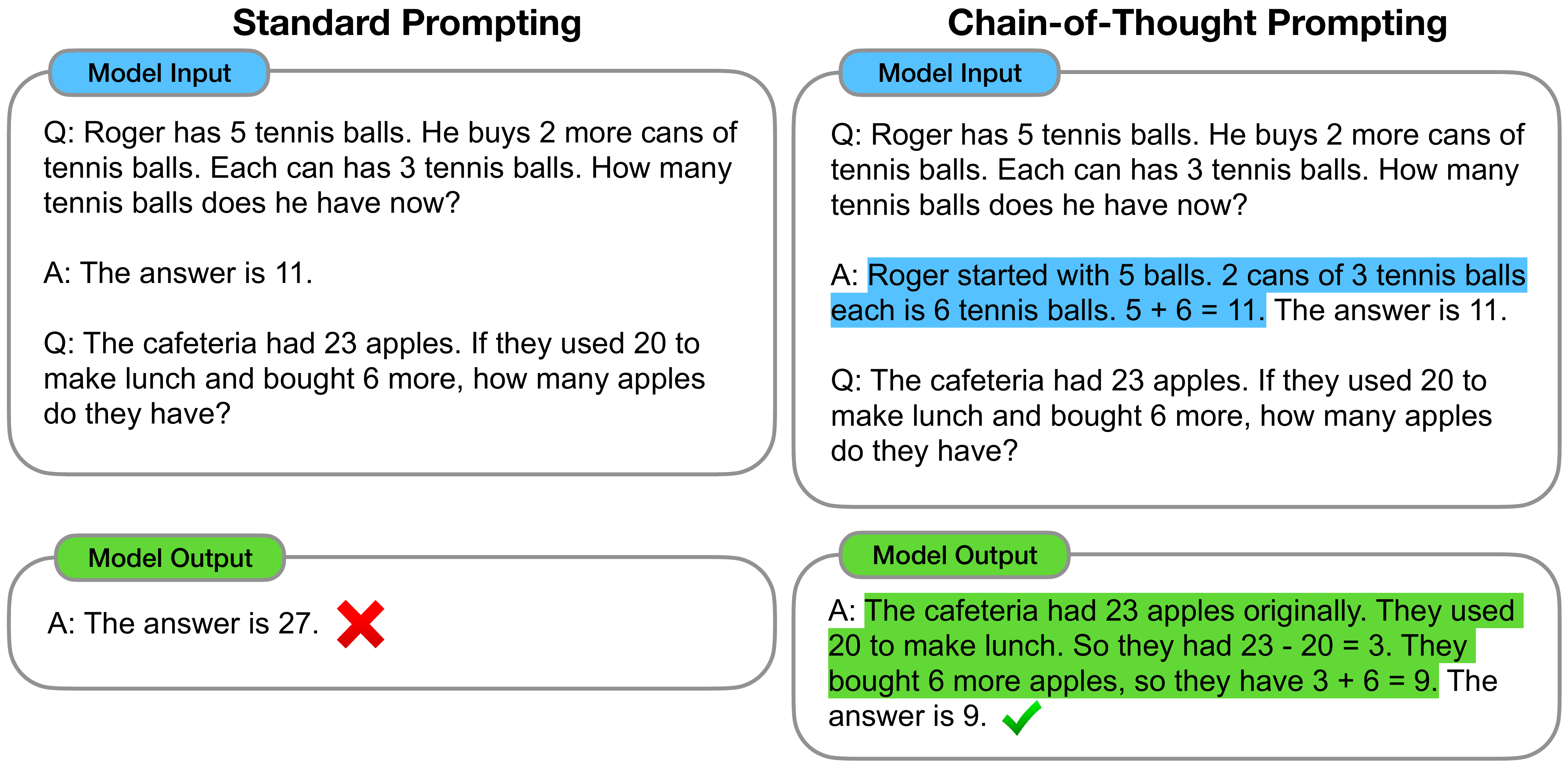
Performance Across Tasks

Example: Math Problem Solving

Input: “Roger has 5 tennis balls. He buys 2 more cans of tennis balls. Each can has 3 tennis balls. How many tennis balls does he have now?”

Standard Prompting: “7 tennis balls”

Chain of Thought Prompting: “Roger starts with 5 tennis balls. He buys 2 cans, and each can has 3 tennis balls. So he gets 2 × 3 = 6 more tennis balls. In total, he has 5 + 6 = 11 tennis balls.”

Few-shot Chain of Thought

  1. Provide examples with step-by-step reasoning
  2. Present new problem without reasoning
  3. Model generates intermediate steps + final answer

Example:

Q: Roger has 5 tennis balls. He buys 2 more cans of tennis balls. 
   Each can has 3 tennis balls. How many tennis balls does he have now?

A: Roger started with 5 balls. 2 cans of 3 tennis balls each is 
   6 tennis balls. 5 + 6 = 11. The answer is 11.

How do Models Learn CoT?

  • Emergent Ability: Appears in sufficiently large models (e.g., GPT-3 175B in Wei et al., 2022)
  • Supervised Fine-tuning: Training on datasets with reasoning steps
  • Reinforcement Learning: Rewarding correct reasoning chains

Experimental Results: Wei et al. (2022)

Task Type Standard Prompting Chain-of-thought Improvement
Arithmetic Reasoning (GSM8K) 17.9% 58.1% +40.2%
Commonsense Reasoning (StrategyQA) 54.4% 69.4% +15.0%
Symbolic Reasoning (Last Letter Concatenation) 34.0% 76.0% +42.0%

Biggest gains on tasks requiring multi-step reasoning

Zero-Shot Chain of Thought (Kojima et al., 2022)

Zero-Shot CoT Overview

Inference for CoT

  • Our goal of inference is either
    • Sampling: \(\tilde{y} \sim P(y \mid x)\) or
    • Mode-seeking Search: \(\hat{y} = \arg\max_y P(y \mid x)\)
  • Sampling is straightforward:
    • sample \(\tilde{z} \sim P(z \mid x)\)
    • sample \(\tilde{y} \sim P(y \mid \tilde{z}, x)\)
  • Mode-seeking is harder

Mode-seeking Search for CoT

  • A first attempt: try to find argmax jointly over \(z, y\)
    • \(\hat{z}, \hat{y} = \arg\max_{z, y} P(z, y \mid x)\)
  • Problem: argmax over \(z, y\) may not give the best \(y\)
    • e.g., if multiple \(z\) lead to the same correct \(y\)

How many inches in 3 feet?

\(z\) \(y\) \(P(z, y \mid x)\)
12 inches in 3 feet, 12*3= 36 0.3
100 cm in a meter, 100*3= 300 0.4
Simple, 36 0.3

Self-Consistency: Wang et al. (2022)

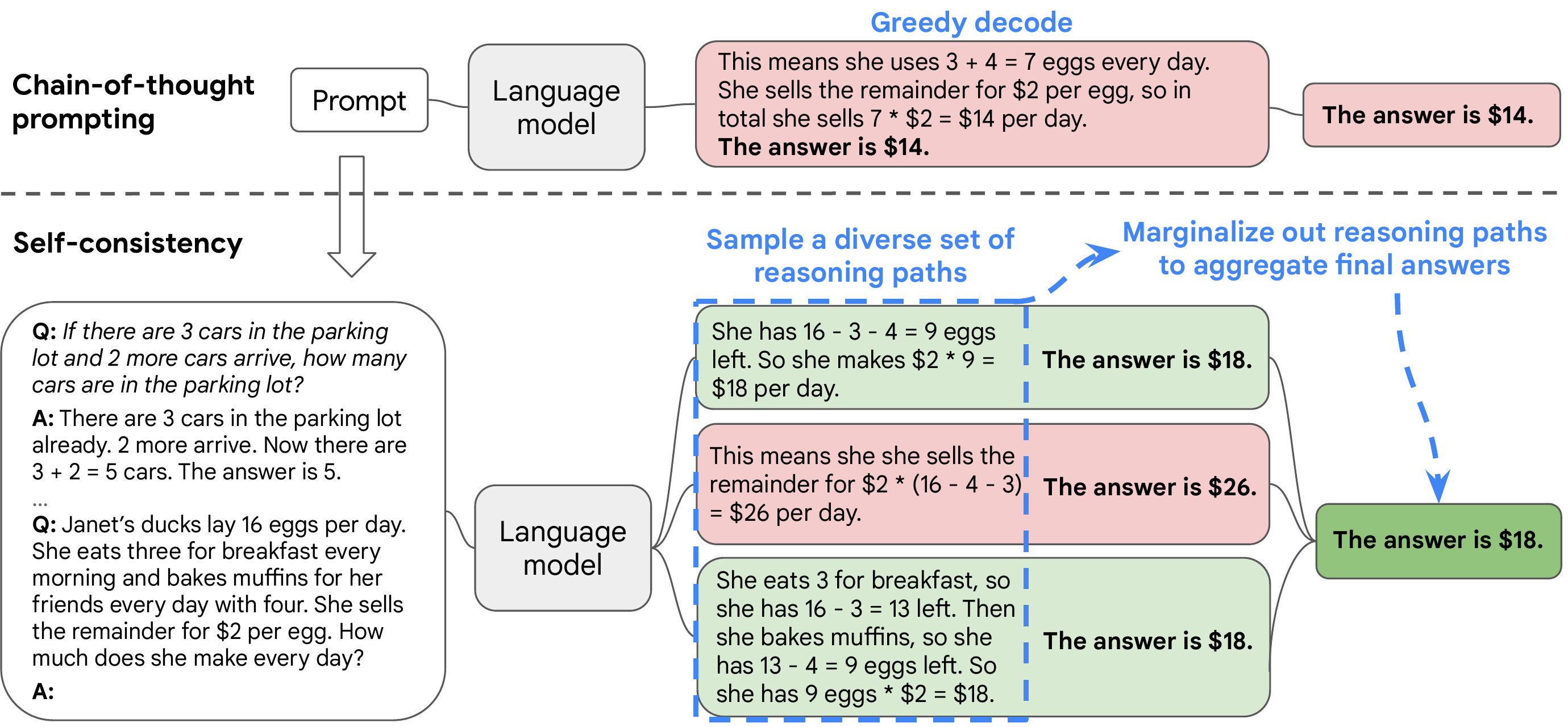
Self-Consistency Method

Self-Consistency: Results

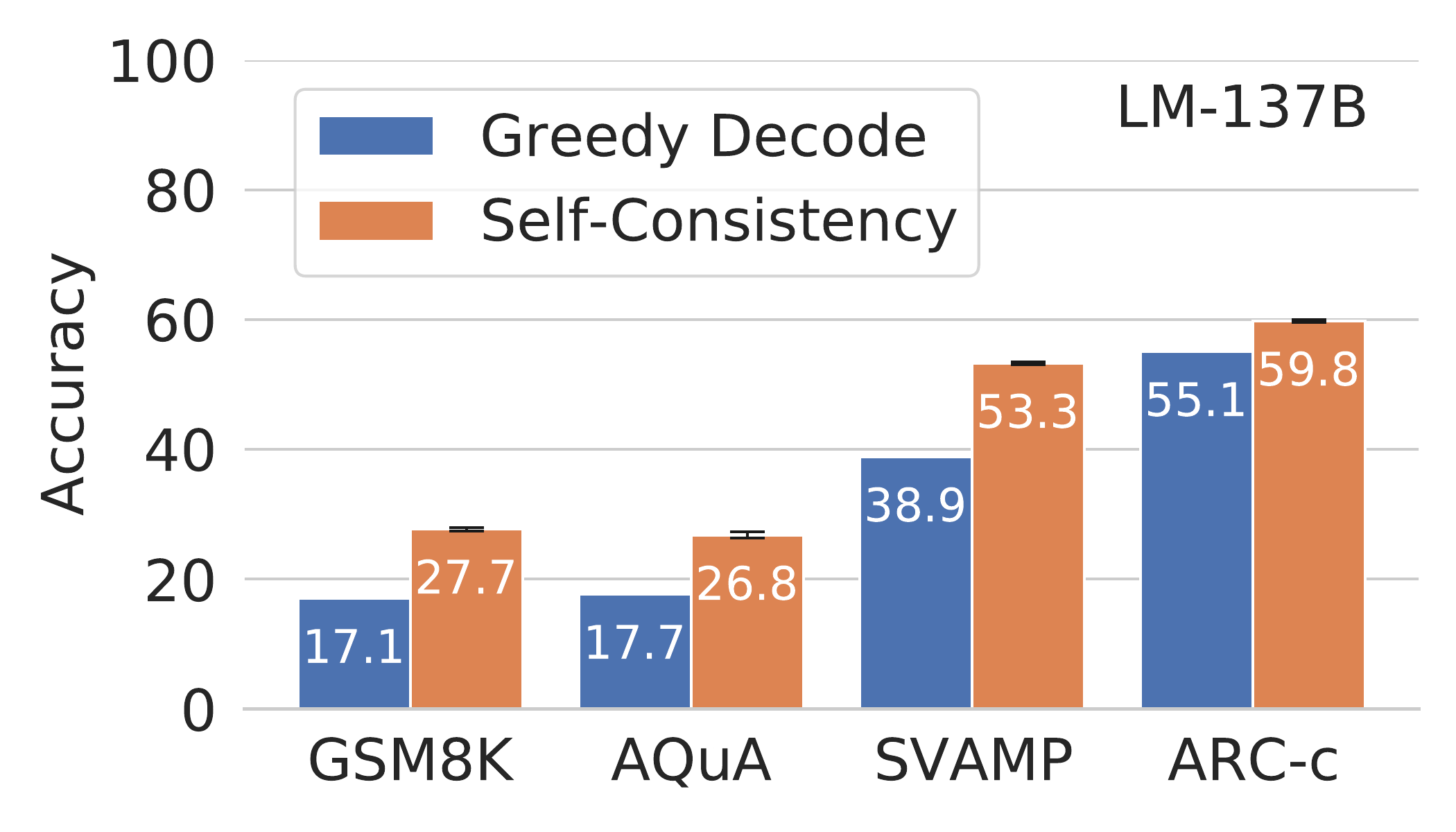
Performance Comparison

Adaptive Self-consistency (Aggarwal et al., 2023)

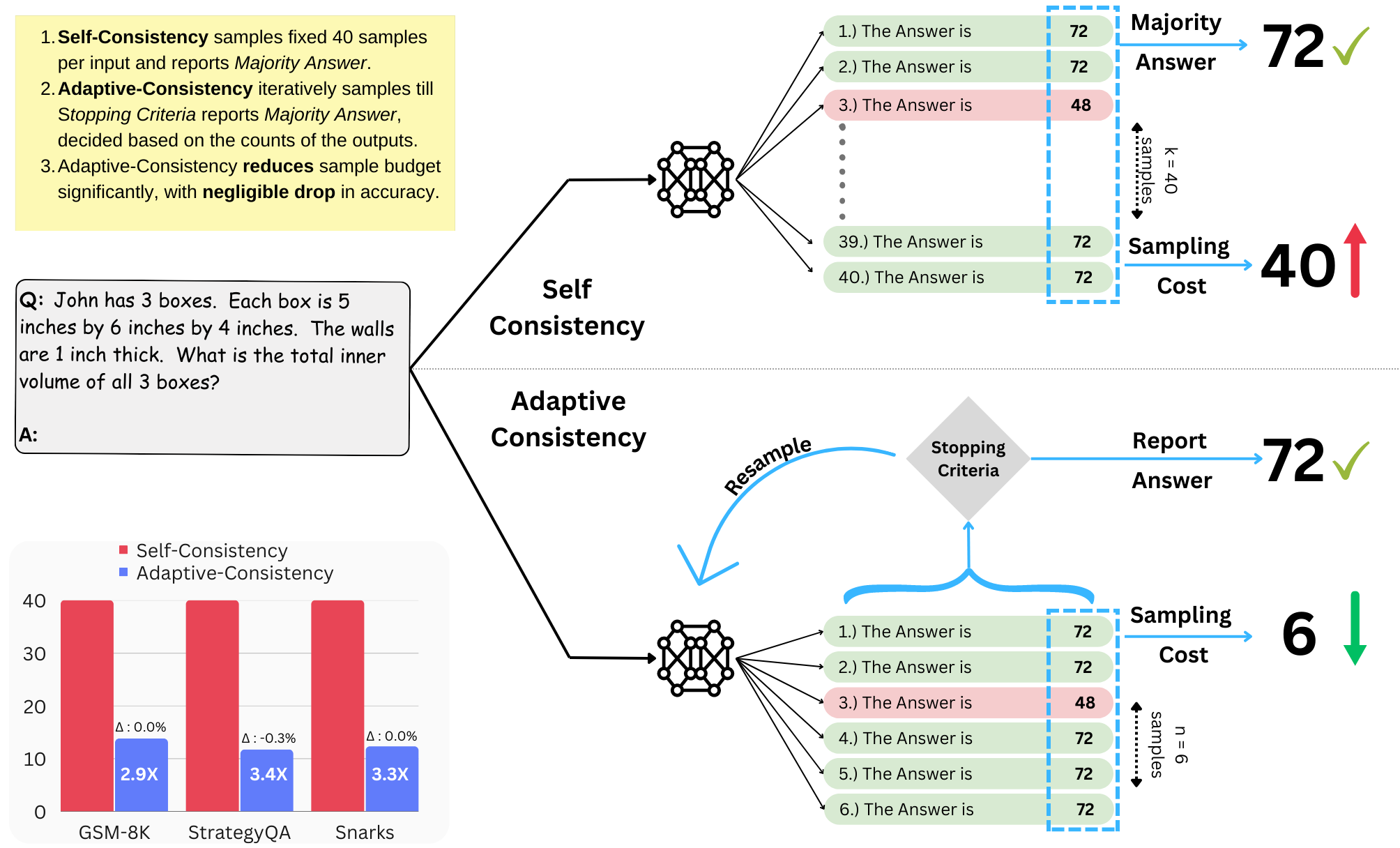
Adaptive Consistency Teaser

Adaptive Self-consistency: Method

Gradually generate samples, stopping when possibility of agreement is high

Stopping Criterion (Beta approximation):

\[\int_{0}^{0.5} p_2^{v_2} \cdot (1 - p_2)^{v_1} dp_2 > C_{thresh}\]

Where \(v_1\) = count of majority answer, \(v_2\) = count of second most frequent answer, \(C_{thresh} = 0.95\)

Results:

  • 7.9x reduction in sample budget
  • <0.1% accuracy drop on average

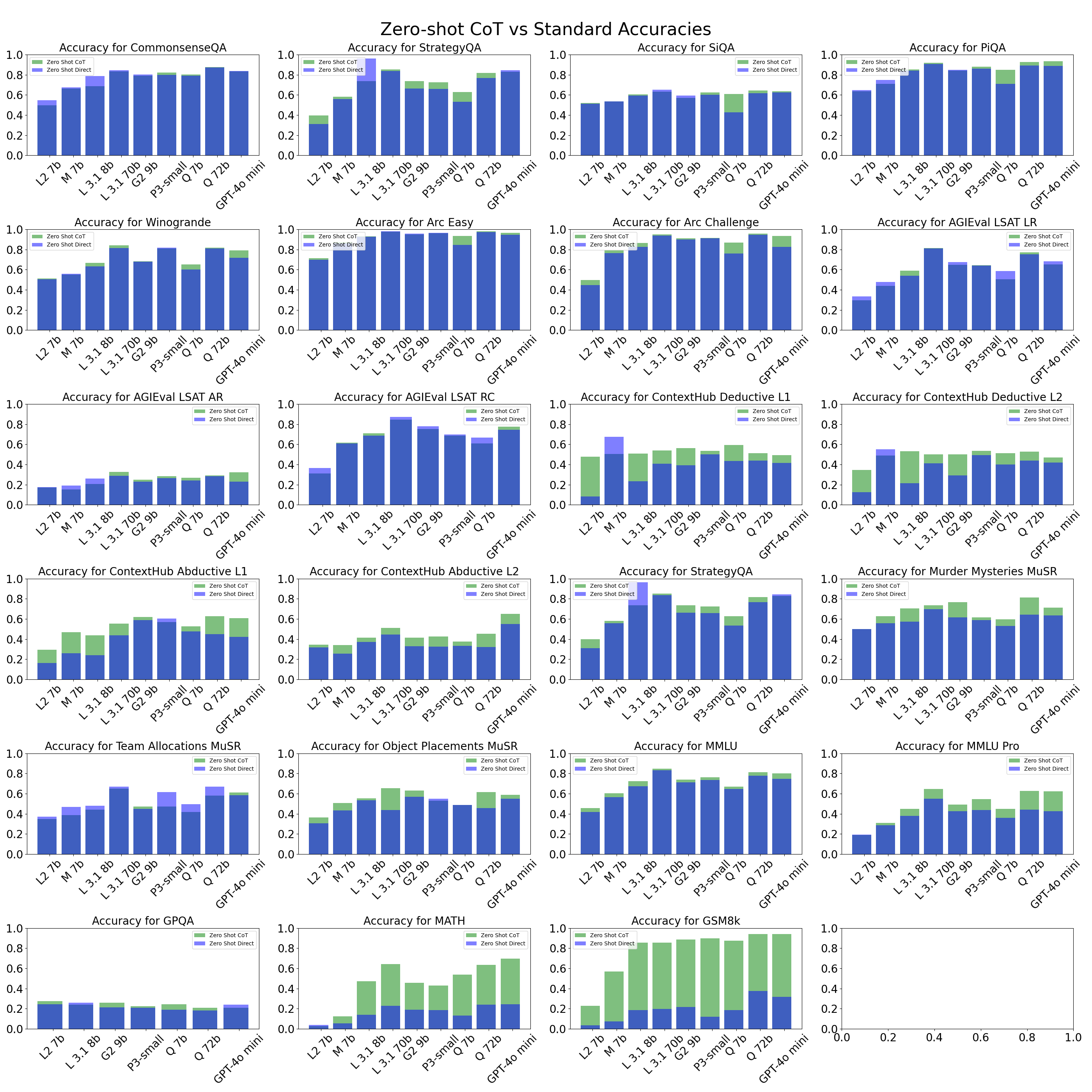
Features of CoT: It is not universally useful (Sprague et al., 2024)

Key Finding: CoT gives strong performance benefits primarily on tasks involving math or logic

Empirical Analysis:

  • Meta-analysis covering 100+ papers using CoT
  • Evaluation of 20 datasets across 14 models

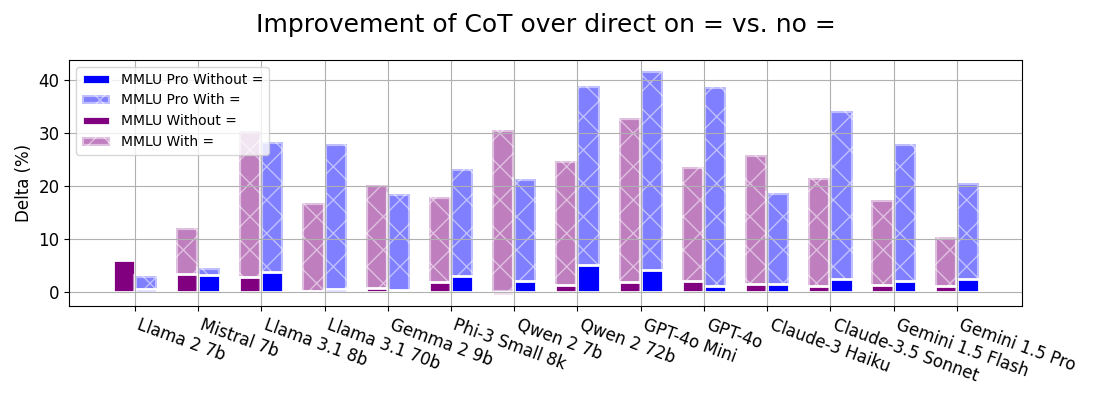
MMLU Results:

  • Direct answering ≈ CoT accuracy unless question contains “=” sign
  • “=” sign indicates symbolic operations and reasoning

CoT Performance by Dataset

CoT Performance by Dataset

CoT Performance: Equals Sign Analysis

Equals Sign Performance

CoT Limitation: Are explanations faithful? (Turpin et al., 2023)

Research Question: Do Chain-of-Thought explanations reflect the model’s true reasoning process?

Experimental Method:

  1. Introduce subtle biases that influence model predictions (e.g., reorder multiple-choice options)
  2. Ask models for CoT explanations of their biased predictions
  3. Test faithfulness: Do explanations mention the biasing factors that actually influenced decisions?

CoT Faithfulness: Results

Faithfulness Overview

Key Findings:

  • 36% accuracy drop when models are biased toward wrong answers (GPT-3.5, Claude 1.0)
  • Models generate confident explanations for both correct and incorrect biased answers
  • Explanations systematically omit mention of the actual biasing factors

Features of CoT: Longer CoTs tend to be better (Fu et al., 2022)

Key Insight: Prompts with higher reasoning complexity (more reasoning steps) achieve substantially better performance

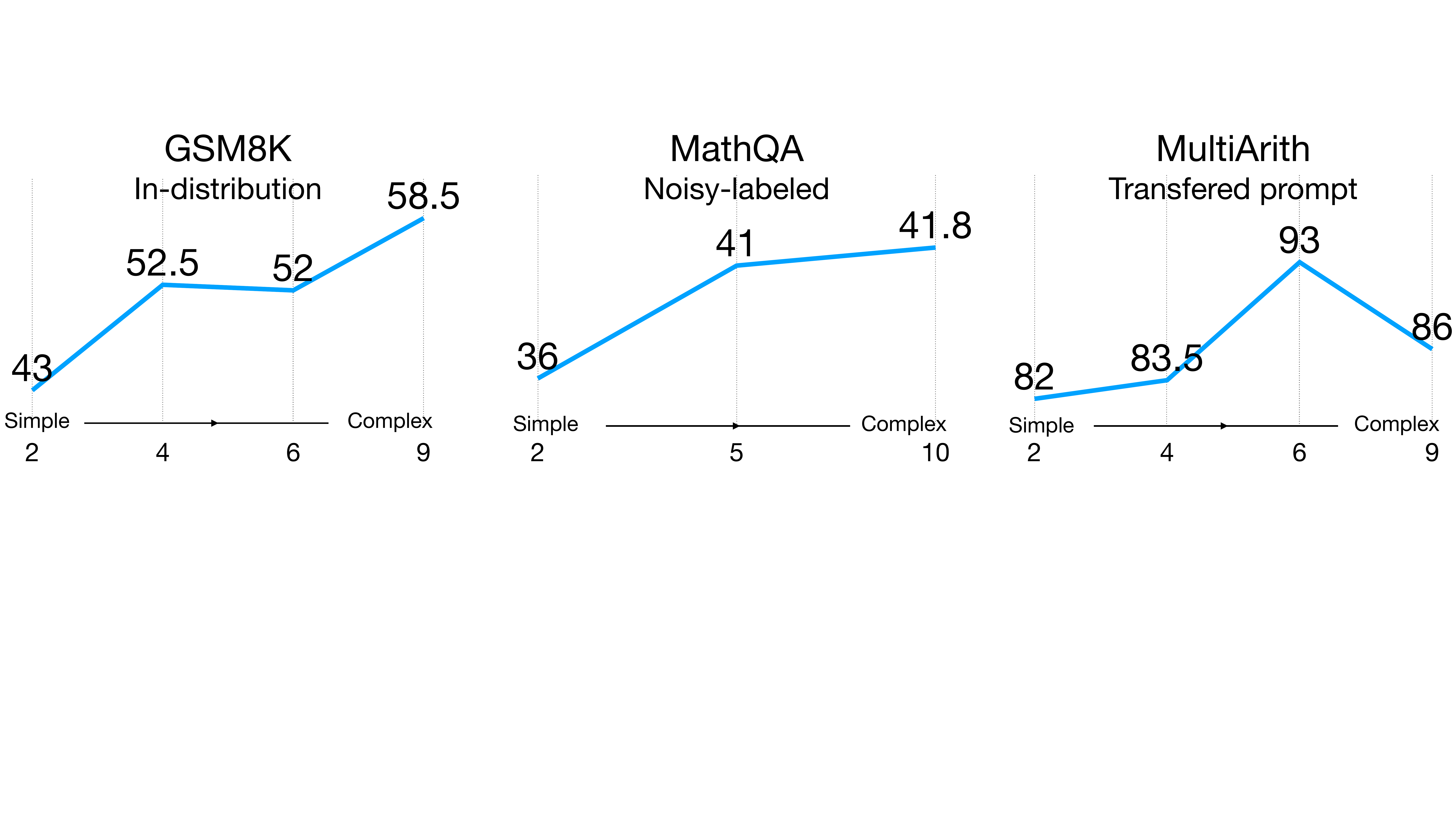
Accuracy vs Reasoning Steps

Complexity-Based Prompting: Method and Results

Complexity-Based Prompting Method

Results:

  • +5.3 to +18 accuracy improvements on average (GSM8K, MultiArith, MathQA)
  • Robust under format perturbation and distribution shift

Features of CoT: It can be used multimodally (Zhang et al., 2023)

Key Innovation: Incorporates both language (text) and vision (images) into CoT reasoning

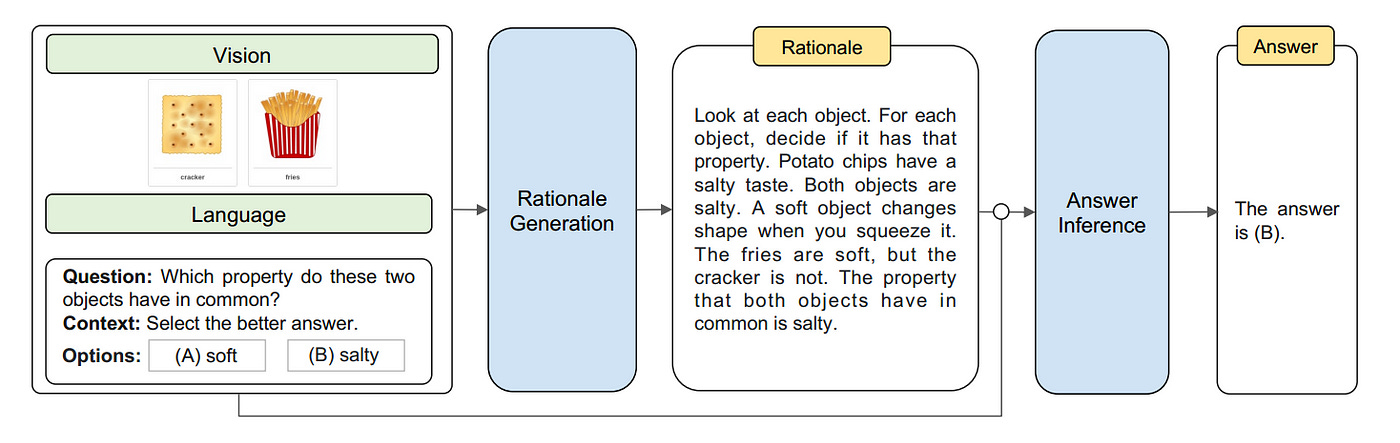
Multimodal CoT Framework

Two-Stage Framework:

  1. Rationale Generation: Generate reasoning chains based on multimodal information
  2. Answer Inference: Leverage better rationales that incorporate visual information

Results:

  • SOTA performance on ScienceQA benchmark with model <1B parameters
  • Outperforms text-only CoT on multimodal reasoning tasks
  • Evaluated on ScienceQA and A-OKVQA benchmarks

Summary

Key Takeaways:

  1. Chain of Thought enables complex reasoning through intermediate steps
  2. Emergent ability that scales with model size
  3. Multiple variants for different use cases (Zero-shot, Self-Consistency)
  4. Significant improvements on reasoning tasks (+17-40% accuracy)
  5. Trade-offs between accuracy and computational cost

Impact: Fundamental technique that has transformed how we approach reasoning with LLMs

Next Class: Self-refine and self-correction methods

Paper Presentations

Today’s Papers:

  1. Least-to-Most Prompting Enables Complex Reasoning in Large Language Models

  2. Chain-of-Thought Reasoning Without Prompting

References

Core Chain-of-Thought Papers:

  • Wei et al. (2022). Chain-of-Thought Prompting Elicits Reasoning in Large Language Models. NeurIPS.
  • Kojima et al. (2022). Large Language Models are Zero-Shot Reasoners. NeurIPS.
  • Wang et al. (2022). Self-Consistency Improves Chain of Thought Reasoning in Language Models. ICLR.

Adaptive Computation Time:

  • Graves (2016). Adaptive Computation Time for Recurrent Neural Networks. arXiv:1603.08983
  • Banino et al. (2021). PonderNet: Learning to Ponder. arXiv:2107.05407
  • Kaya et al. (2019). DeeBERT: Dynamic Early Exiting for Accelerating BERT Inference. ACL.
  • Zhou et al. (2020). BERT Loses Patience: Fast and Robust Inference with Early Exit. NeurIPS.

CoT as Adaptive Computation:

  • Manglik (2024). When to Think Step by Step: Computing the Cost–Performance Trade-offs of Chain-of-Thought Prompting.
  • Wu et al. (2024). An Empirical Analysis of Compute-Optimal Inference for Problem-Solving with Language Models. arXiv:2408.00724
  • Sardana et al. (2024). Beyond Chinchilla-Optimal: Accounting for Inference in Language Model Scaling Laws. arXiv:2401.00448

Additional CoT Research:

  • Aggarwal et al. (2023). Adaptive-Consistency: A Cost-Efficient, Model-Agnostic Technique. EMNLP. arXiv:2305.11860
  • Sprague et al. (2024). To CoT or not to CoT? Chain-of-thought helps mainly on math and logic. ICLR. arXiv:2409.12183
  • Turpin et al. (2023). Language Models Don’t Always Say What They Think. NeurIPS. arXiv:2305.04388
  • Fu et al. (2022). Complexity-Based Prompting for Multi-step Reasoning. arXiv:2210.00720
  • Zhang et al. (2023). Multimodal Chain-of-Thought Reasoning in Language Models. TMLR. arXiv:2302.00923

Paper Presentations:

  • Zhou et al. (2022). Least-to-Most Prompting Enables Complex Reasoning in Large Language Models. ICLR 2023. arXiv:2205.10625
  • Wang & Zhou (2024). Chain-of-Thought Reasoning Without Prompting. arXiv:2402.10200

Questions + Discussion

Carnegie Mellon University - Language Model Inference - Fall 2025