Self-Refine and Self-Correction Methods
Graham Neubig


Motivation: Why Self-Correction?
- LLMs generation in a single pass left to right
- Susceptible to errors in long or complex outputs
- Contrast – human iterative writing
Self-correction Process
def self_correction(x, max_iterations=3):
y = generate(x) # Initial generation
for i in range(max_iterations):
critique = evaluate(y, x) # Evaluate current output
if is_satisfactory(critique):
break
y = refine(y, critique, x) # Improve based on critique
return y
Design Decisions
- Critique: explicit or implicit
- Training: without or with
- Conditioning: \(x\), \(y_n\), \(c_n\)
- Tools: none, optional, or required
Comparison of Self-Correction Methods
| Method | Critique | Training | Conditioning | Tools | Key Strength |
|---|---|---|---|---|---|
| Deliberation Networks | ❌ None | ✅ With | \(x\), \(y_n\) | ❌ None | RL-based Training |
| Modeling Edit Processes | ❌ None | ✅ With | \(x\), \(y_n\) | ❌ None | Models full editing workflow |
| Edit Representations | ⚡ Implicit | ✅ With | \(x\), \(h\) | ❌ None | Learns edit semantics |
| Self-Refine | ✅ Explicit | ❌ Without | \(x\), \(y_n\), \(c_n\) | ❌ None | Simple, broadly applicable |
| Self Debug | ✅ Explicit | ❌ Without | \(x\), \(y_n\), \(c_n\) | ✅ Code Execution | Code-specific debugging |
| Reflexion | ✅ Explicit | ❌ Without | \(x\), \(y_n\), \(c_n\) | ⚠️ Optional | Long-term learning |
| CRITIC | ✅ Explicit | ❌ Without | \(x\), \(y_n\), \(c_n\) | ✅ Required | External verification |
Deliberation Networks
Paper: Deliberation Networks: Sequence Generation Beyond One-Pass Decoding (Xia et al., 2017)
Key Innovation: Two-pass decoding with deliberation and refinement
- First-pass decoder generates initial draft sequence
- Second-pass decoder refines with global context
Deliberation Networks: Algorithm
def deliberation_networks(x):
# First-pass: generate initial draft
y = first_pass_decoder(x)
# Second-pass: refine with full context (no iteration)
y = second_pass_decoder(x, y)
return y
Key Insight: Two-pass refinement with global context, no iterative feedback loop
Deliberation Networks: Training Objective
Training Objective:
Lower Bound Optimization:
Key Training Details:
- Monte Carlo sampling used to approximate intractable gradients
- Both decoders trained jointly with shared encoder
Deliberation Networks: Results
Performance on Neural Machine Translation:
| Dataset | Achievement | Improvement |
|---|---|---|
| WMT’14 En→Fr | 41.5 BLEU | State-of-the-art |
| General Performance | ~1.7 BLEU improvement | Over single-pass baseline |
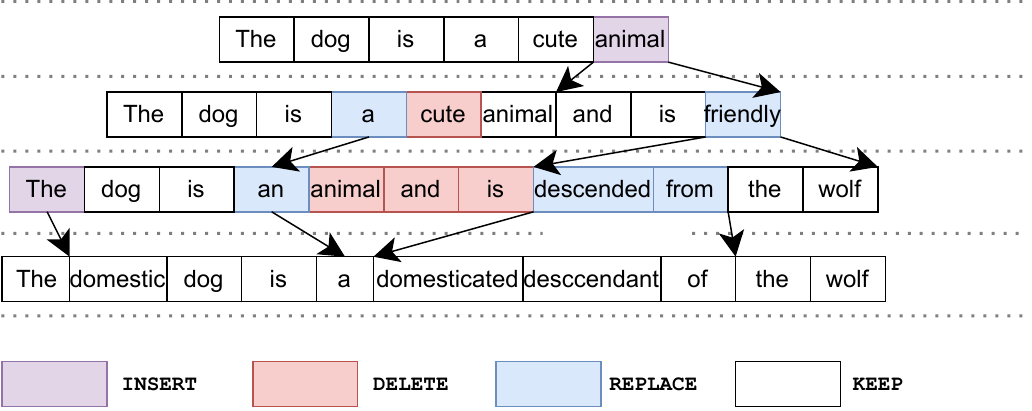
Learning to Model Editing Processes
Paper: Learning to Model Editing Processes (Reid & Neubig, 2021)
Key Innovation: Model the entire multi-step editing process, not just single edits
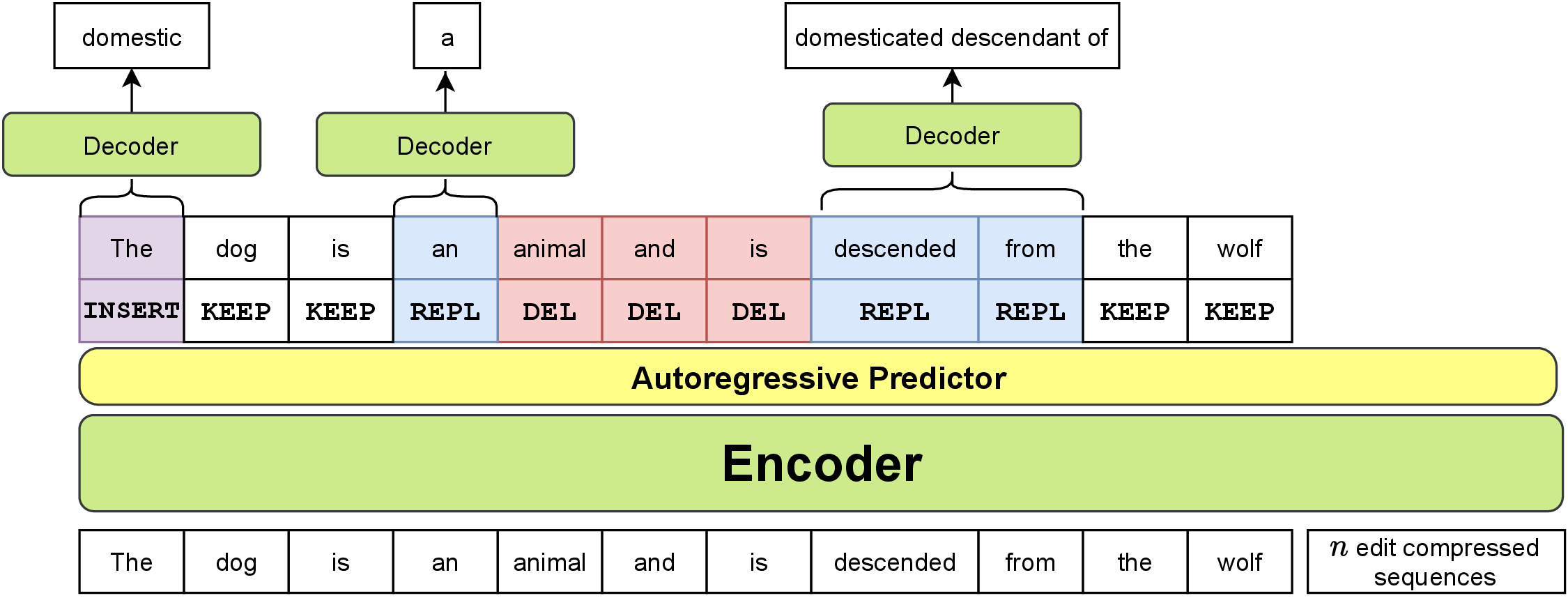
Edit Processes: Algorithm
def edit_processes(x):
edit_history = []
y = "" # Start from blank slate
while not is_complete(y):
# Predict next edit operations (INSERT, DELETE, KEEP, REPLACE)
edit_ops = predict_edit_operations(x, y, edit_history)
# Generate content for operations that need it
content = generate_content(x, y, edit_ops, edit_history)
# Apply edits to current text
y = apply_edits(y, edit_ops, content)
edit_history.append((edit_ops, content))
return y
Key Insight: Multi-step editing workflow from blank slate, models complete edit sequences
Edit Processes: Details
Core Decomposition:
Edit Decoding:
Edit Processes: Results
| Dataset | Single-Order | 2-Order | Improvement |
|---|---|---|---|
| WikiRevisions | 57.31 ePPL | 53.91 ePPL | -3.4 ePPL |
| CodeRevisions | 37.57 ePPL | 33.17 ePPL | -4.4 ePPL |
Key Findings:
- 22.9% relative perplexity reduction over state-of-the-art editing baseline
- Multi-step context crucial for predicting non-KEEP operations
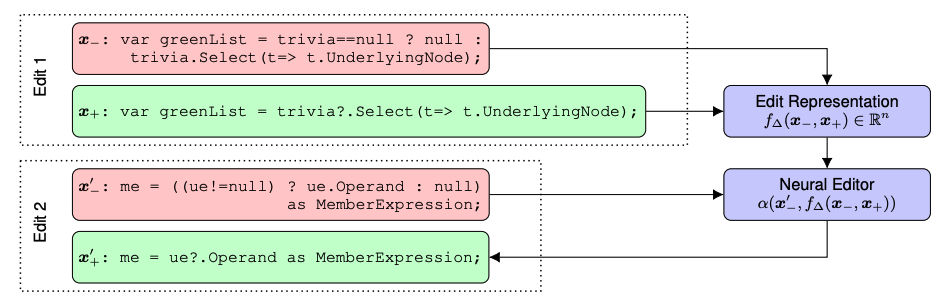
Learning to Represent Edits
Paper: Learning to Represent Edits (Yin et al., 2019)
Key Innovation: Learn distributed representations of edit operations
Edit Representations: Algorithm
def edit_representations(source, target):
# Encode the edit operation between source and target
edit_vector = edit_encoder(source, target)
# Apply learned edit to new source text
def apply_edit(new_source):
return neural_editor(new_source, edit_vector)
return apply_edit
Key Insight: Learn semantic edit representations that generalize across different texts
Edit Representations: Details
Architecture Components:
- Edit Encoder: BiLSTM processes aligned token sequences with diff symbols (+, -, ↔, =)
- Neural Editor: Seq2seq with attention and copying mechanism
- Bottleneck constraint: Edit representation limited to 512 dimensions
Training Objective:
Edit Representations: Results
Performance on Edit Similarity:
| Model | DCG@3 | NDCG@3 | Accuracy@1 |
|---|---|---|---|
| Bag of Words | 7.77 | 75.99% | 58.46% |
| Edit Encoder | 10.09 | 90.05% | 75.90% |
Self-Refine
Paper: Self-Refine: Iterative Refinement with Self-Feedback (Madaan et al., 2023)
Key Innovation: Training-free iterative improvement using self-generated feedback
Self-Refine: Algorithm
def self_refine(x, max_iterations=3):
y = generate(x) # Initial generation
for i in range(max_iterations):
critique = self_feedback(y, x) # Generate self-critique
if is_satisfactory(critique):
break
y = refine(y, critique, x) # Improve based on critique
return y
Key Insight: Single LLM handles generation, self-critique, and refinement through prompting
Self-Refine: Generation and Feedback
Prompt-Based Components:
generate(x) - Initial Generation
-
Standard few-shot prompting
-
Task-specific examples provided
self_feedback(y, x) - Critique Generation
-
Prompt: “Why is this [output] not [target quality]?”
-
Identifies specific improvement areas
Self-Refine: Refinement and Stopping
Iterative Improvement:
refine(y, feedback, x) - Iterative Improvement
-
Combines original input, current output, and feedback
-
Prompt: “Improve the [output] based on this feedback”
is_satisfactory(feedback) - Stopping Criterion
-
Simple heuristic: check for positive feedback
-
Or fixed number of iterations (typically 2-3)
Key Insight: Single LLM handles all components through different prompting strategies
Self-Refine: Main Results
| Task | GPT-3.5 | GPT-3.5 + Self-Refine | GPT-4 | GPT-4 + Self-Refine |
|---|---|---|---|---|
| Sentiment Reversal | 8.8% | 30.4% (+21.6) | 3.8% | 36.2% (+32.4) |
| Dialogue Response | 36.4% | 63.6% (+27.2) | 25.4% | 74.6% (+49.2) |
| Code Optimization | 14.8% | 23.0% (+8.2) | 27.3% | 36.0% (+8.7) |
| Code Readability | 37.4% | 51.3% (+13.9) | 27.4% | 56.2% (+28.8) |
| Math Reasoning | 64.1% | 64.1% (0) | 92.9% | 93.1% (+0.2) |
| Acronym Generation | 41.6% | 56.4% (+14.8) | 30.4% | 56.0% (+25.6) |
| Constrained Generation | 28.0% | 37.0% (+9.0) | 15.0% | 45.0% (+30.0) |
Self Debug
Paper: Teaching Large Language Models to Self-Debug (Chen et al., 2023)
Key Innovation: Code-specific self-correction with execution feedback

Self Debug: Algorithm
def self_debug(x, max_iterations=3):
y = generate(x) # Initial code generation
for i in range(max_iterations):
# Execute code and get objective feedback
result, error = execute_code(y, test_cases)
if result == "PASS":
break
# Generate explanation and fix based on execution error
critique = explain_error(y, error, x)
y = refine(y, critique, x)
return y
Key Insight: Execution feedback provides objective critique for iterative code improvement
Self Debug: Results
| Dataset | Model | Baseline | Self Debug | Improvement |
|---|---|---|---|---|
| Spider (SQL) | GPT-4 | 73.2% | 73.6% | +0.4% |
| TransCoder | GPT-4 | 77.3% | 90.4% | +13.1% |
| MBPP (Python) | GPT-4 | 72.8% | 80.6% | +7.8% |
Key Findings:
- Significant improvements on code translation tasks
- Execution feedback more effective than simple prompting
- 1 sample with Self-Debug matches 16 samples without
Reflexion
Paper: Reflexion: Language Agents with Verbal Reinforcement Learning (Shinn et al., 2023)
Key Innovation: Memory-augmented self-improvement for agents
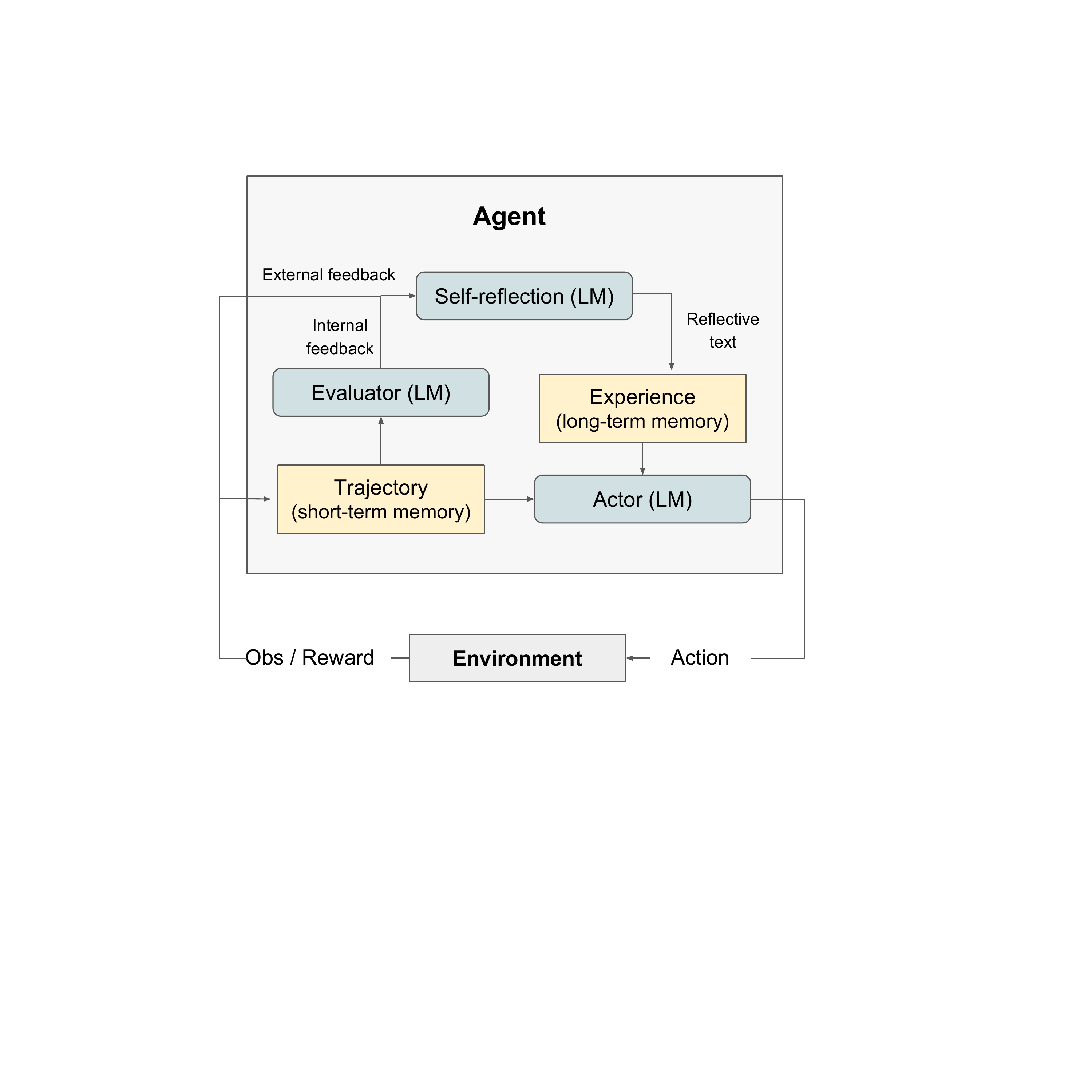
Reflexion: Algorithm
def reflexion(x, max_trials=3):
memory = []
for trial in range(max_trials):
# Generate trajectory using current memory
y = generate(x, memory)
# Evaluate performance with external reward
reward = evaluate(y, x)
if reward >= success_threshold:
return y
# Generate self-reflection and store in memory
critique = self_reflect(y, x, reward)
memory.append(critique)
return y
Key Insight: Memory-augmented self-improvement through verbal reflection on failures
Reflexion: Results
Performance Across Domains:
| Task | Baseline | Reflexion | Improvement |
|---|---|---|---|
| HumanEval (Code) | 80% | 91% | +11% |
| AlfWorld (Decision) | 75% | 97% | +22% |
| HotPotQA (Reasoning) | 51% | 74% | +23% |
CRITIC
Paper: CRITIC: Large Language Models Can Self-Correct with Tool-Interactive Critiquing (Gou et al., 2023)
Key Innovation: Combine self-correction with external tool verification
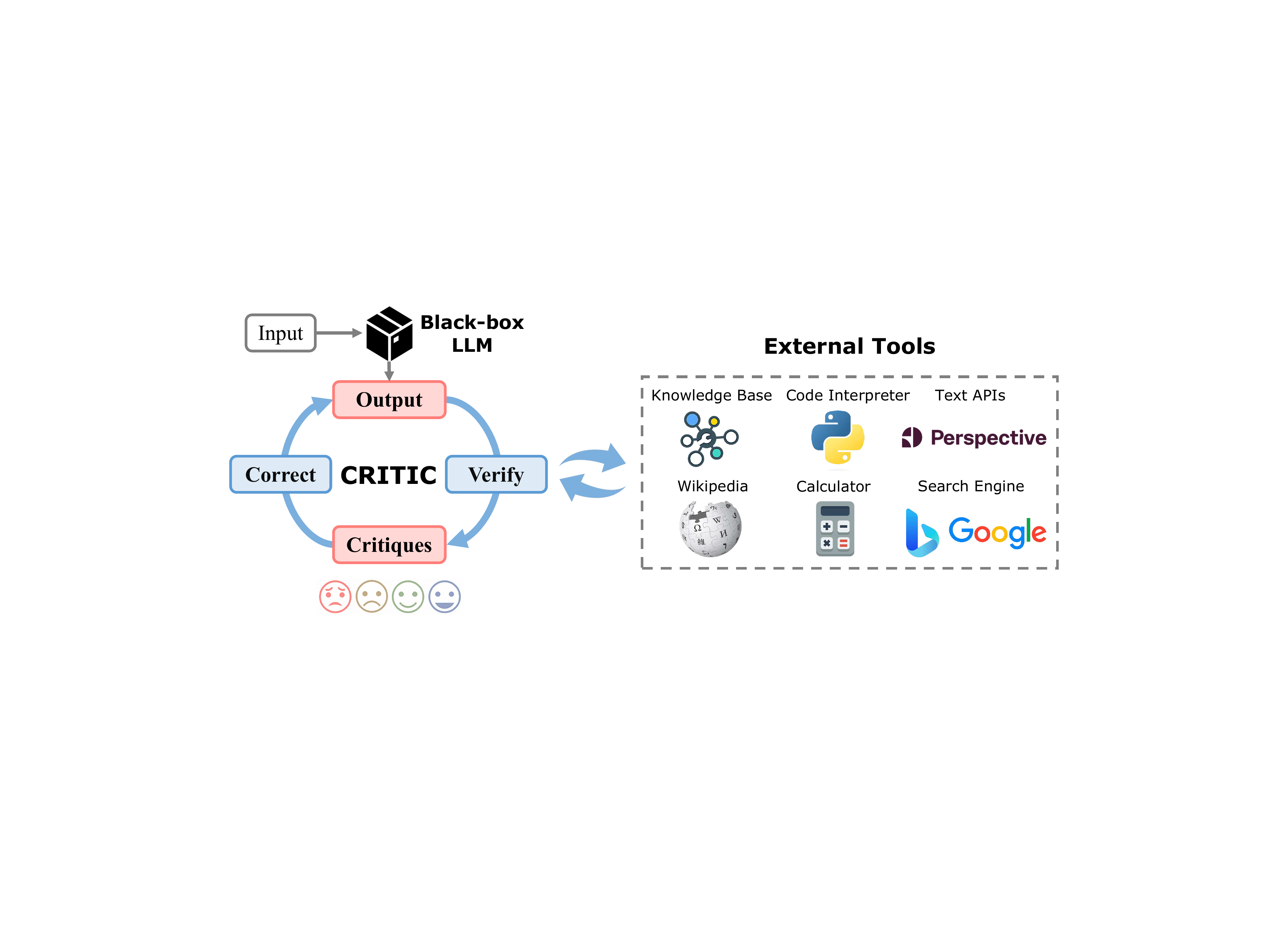
CRITIC: Algorithm
def critic(x, max_iterations=3):
y = generate(x) # Initial generation
for i in range(max_iterations):
# Use external tools to verify/critique
critique = tool_critique(y, x)
if critique.is_correct:
break
# Refine based on tool feedback
y = refine(y, critique, x)
return y
Key Insight: External tools provide objective verification and specific error feedback
CRITIC: Details
Tool Integration
- Code execution for programming tasks
- Search engines for factual verification
- Calculators for mathematical reasoning
- APIs for real-time information
Key Differentiators
- Objective verification: Tools provide ground truth feedback
- Error detection: Identifies specific mistakes
CRITIC: Results
| Task Domain | Improvement | Key Benefit |
|---|---|---|
| Math Reasoning | Significant gains on GSM8K, SVAMP | Code execution verification |
| Factual QA | +7.7 F1 average (ChatGPT) | Search engine fact-checking |
| Program Synthesis | Enhanced code generation | Runtime error detection |
Limitations of Self-Correction: Critical Analysis
Paper: Large Language Models Cannot Self-Correct Reasoning Yet (Huang et al., 2024)
Key Findings:
- Intrinsic self-correction often fails without external feedback
- Performance may degrade with naive self-correction prompting
- Oracle feedback is often needed for improvements in prior work
Why Self-Correction Fails:
- Limited self-evaluation: Models struggle to identify their own errors
- Confirmation bias: Tendency to reinforce initial reasoning
- Knowledge limitations: Cannot correct what they don’t know
When Does Self-Correction Work?
Successful Scenarios
- Surface-level errors: Grammar, style, formatting
- With external feedback: Code execution, fact-checking
- Strong base models: GPT-4 vs smaller models
Challenging Scenarios
- Deep reasoning errors: Mathematical proofs, logic
- Knowledge gaps: Factual inaccuracies
- Complex multi-step reasoning: Long chains of inference
Takeaway: Self-correction is not a panacea - effectiveness depends heavily on task type and model capabilities
Self-Correction Examples: Success vs Failure

Conclusion
When desiging a self-correction strategy, we think about:
- Critique: explicit or implicit
- Training: without or with
- Conditioning: \(x\), \(y_n\), \(c_n\)
- Tools: none, optional, or required
Next up: Reasoning models that learn self-correction natively in chains-of-thought