Reasoning Models

Graham Neubig

What is a Reasoning Model?

A model trained (usually using RL) to leverage long chains of thought to perform better on tasks

Extended reasoning sequences
Self-correction
Longer sequence generally = better performance
Typically trained with verifiable rewards

STaR: Bootstrapping Reasoning

Early work on training LLMs to reason

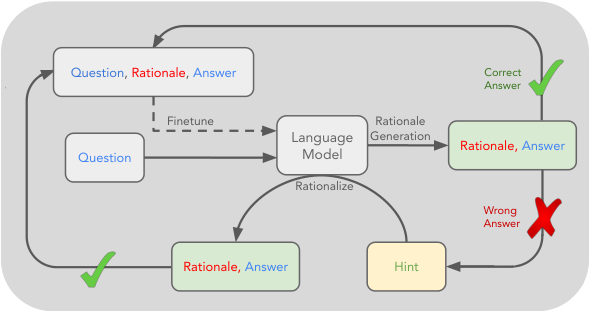
STaR: Algorithm

Generate answers and rationales
Filter correct chains based on reward
- If correct, keep full chain
- If incorrect, generate rationale given answer
Fine-tune on filtered data
Repeat

STaR: Training Objective

RL-style policy gradient objective:

\[J(M, X, Y) = \sum_i \mathbb{E}_{\hat{r}_i, \hat{y}_i \sim p_{M}(\cdot \mid x_i)} \mathbf{1}(\hat{y}_i = y_i)\]

\[\nabla J = \sum_i \mathbb{E}_{\hat{r}_i, \hat{y}_i \sim p_{M}(\cdot \mid x_i)} \left[ \mathbf{1}(\hat{y}_i = y_i) \cdot \nabla \log p_M(\hat{y}_i, \hat{r}_i \mid x_i) \right]\]

Key insight: Filter discards gradients for incorrect reasoning chains

STaR: Experimental Setup

Setup: GPT-J (6B) on arithmetic, CommonsenseQA, GSM8K

Input:
6 2 4 + 2 5 9
Target:
<scratch>
6 2 4 + 2 5 9 , C: 0
2 + 5 , 3  C: 1
6 + 2 , 8 3  C: 0
, 8 8 3  C: 0
0 8 8 3
</scratch>
8 8 3

Training: Iterative filtering and fine-tuning

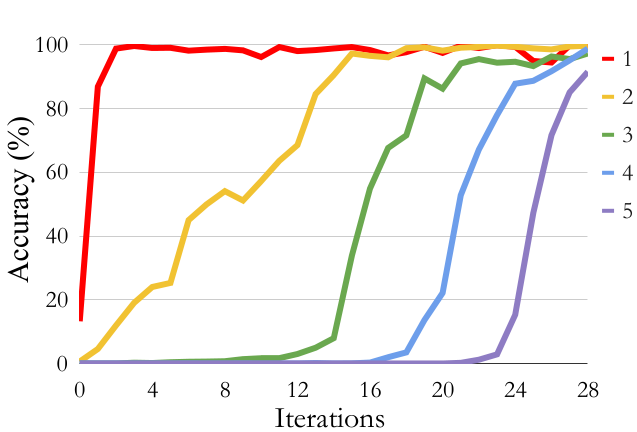
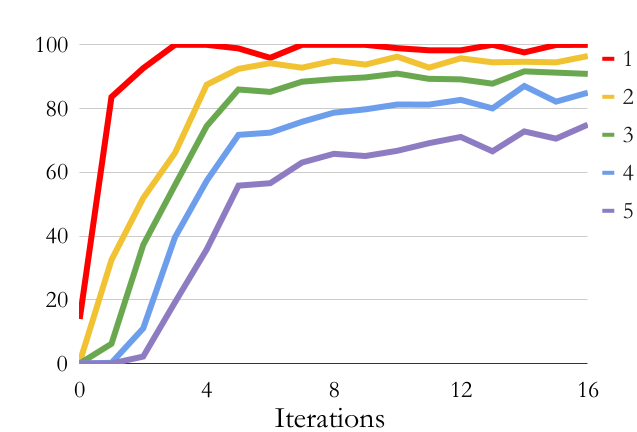
STaR: Digit Addition Results

Without Rationalization

With Rationalization

DeepSeek R1: Overview

Large-scale RL directly on base model (no SFT first)
Group Relative Policy Optimization (GRPO)
Multi-stage pipeline: Cold start → RL → Rejection sampling → Final RL

R1: Group Relative Policy Optimization (GRPO)

Generate outputs in a group:

\[{(o_1, r_1), (o_2, r_2), \ldots, (o_G, r_G) \sim \pi_{\theta_{old}}(\cdot | q)}\]

Use group statistics to compute advantage:

\[A_i = \frac{r_i - \text{mean}(\{r_1, \ldots, r_G\})}{\text{std}(\{r_1, \ldots, r_G\})}\]

Calculate loss:

\[\mathcal{J}_{GRPO}(\theta) = \mathbb{E} \left[ \frac{1}{G}\sum_{i=1}^G \min \left( \frac{\pi_\theta(o_i |q)}{\pi_{\theta_{old}}(o_i |q)} A_i, \text{clip} \left( \frac{\pi_\theta(o_i |q)}{\pi_{\theta_{old}}(o_i |q)}, 1 - \epsilon, 1 + \epsilon \right) A_i \right) \right]\]

R1: Prompt Template

Training template:

Template
A conversation between User and Assistant. The user asks a question, and the Assistant solves it. The assistant first thinks about the reasoning process in the mind and then provides the user with the answer. The reasoning process and answer are enclosed within <think> </think> and <answer> </answer> tags, respectively. User: prompt. Assistant:

Design principles: Minimal structural constraints, no content bias

R1: Accuracy Transition

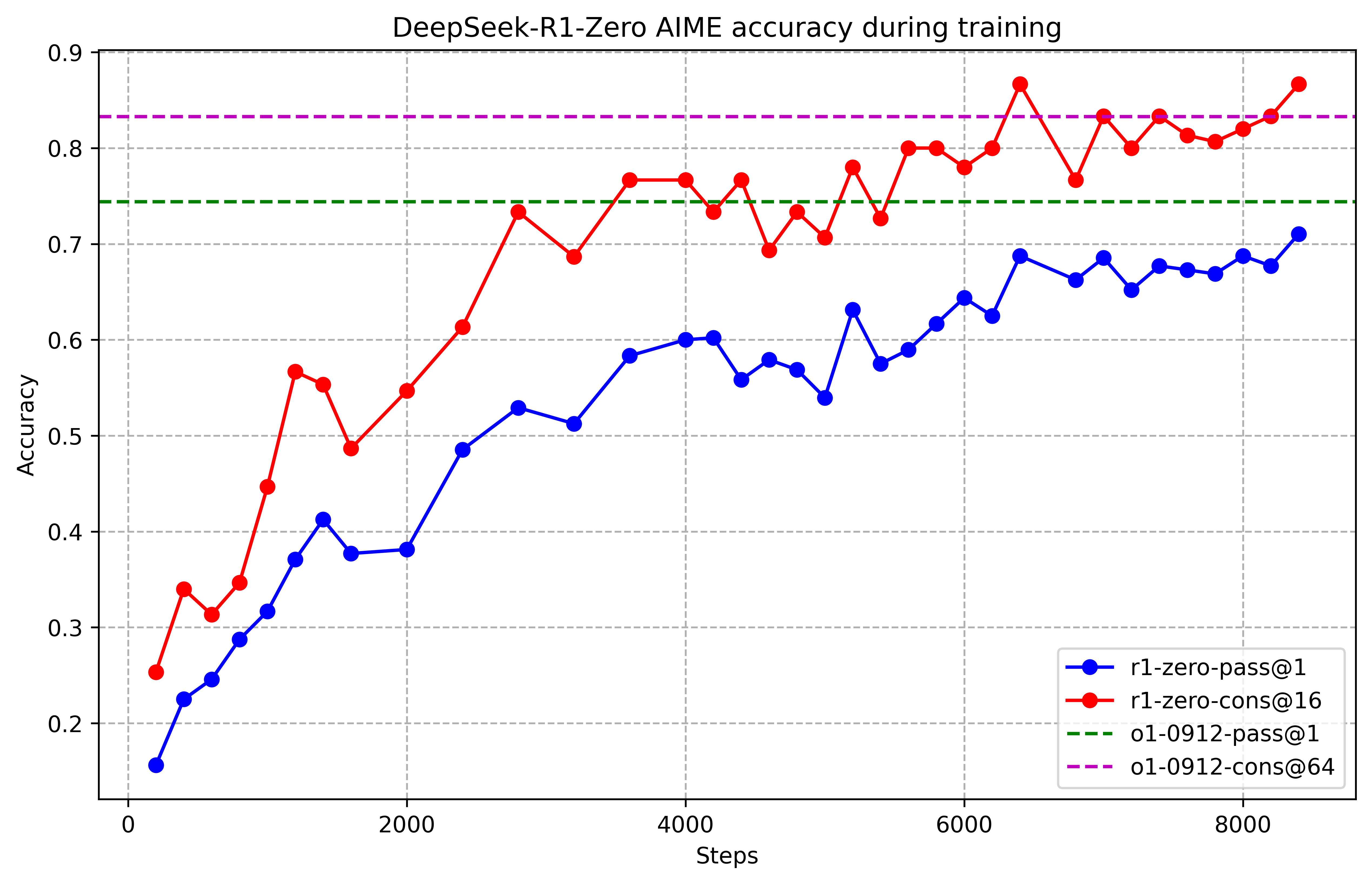
AIME 2024 performance: 15.6% → 71.0% (pass@1), 86.7% (majority voting)

R1: Length Transition

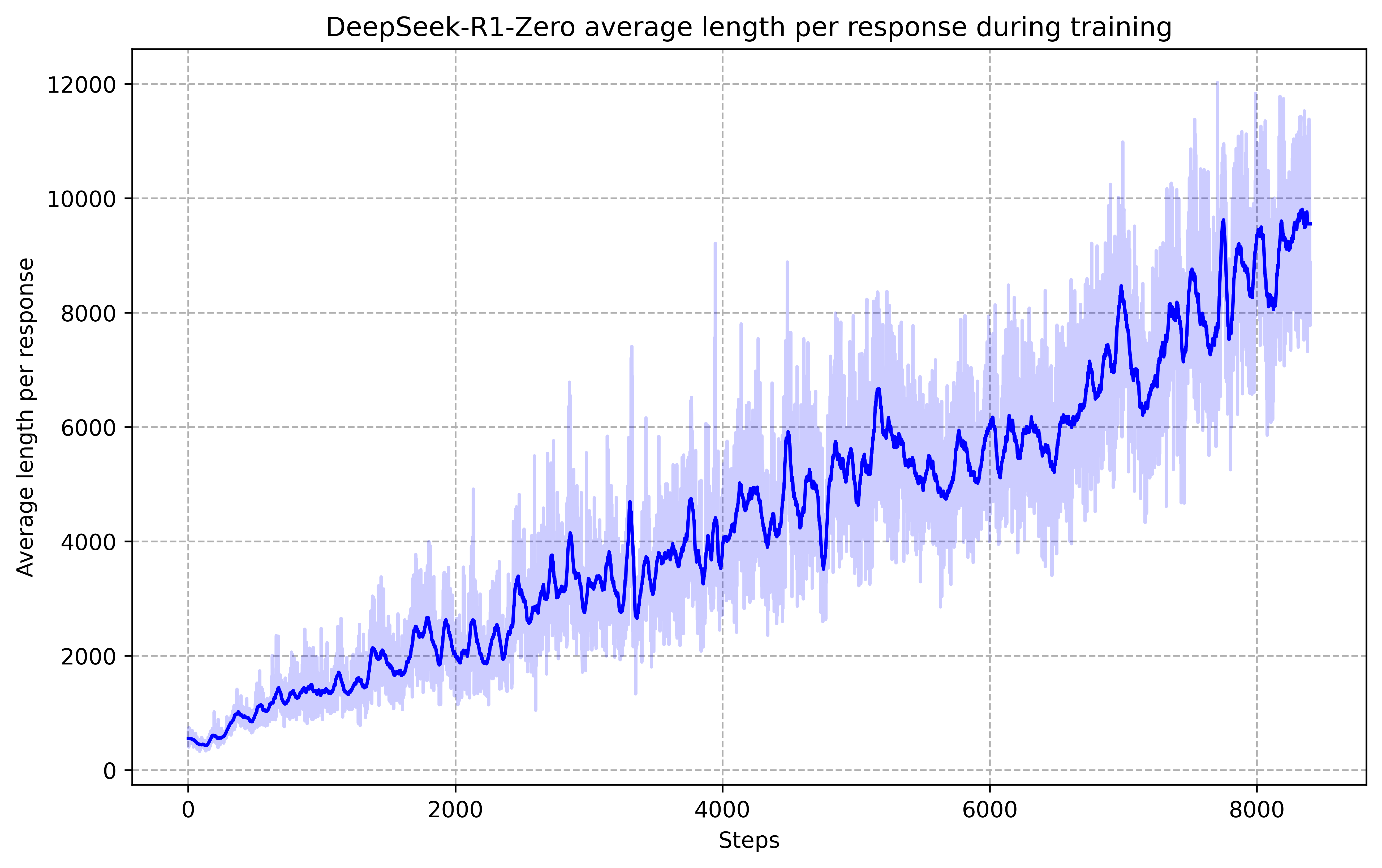
Thinking time naturally increases from hundreds to thousands of tokens

R1: The “Aha Moment”

R1: Distillation Results

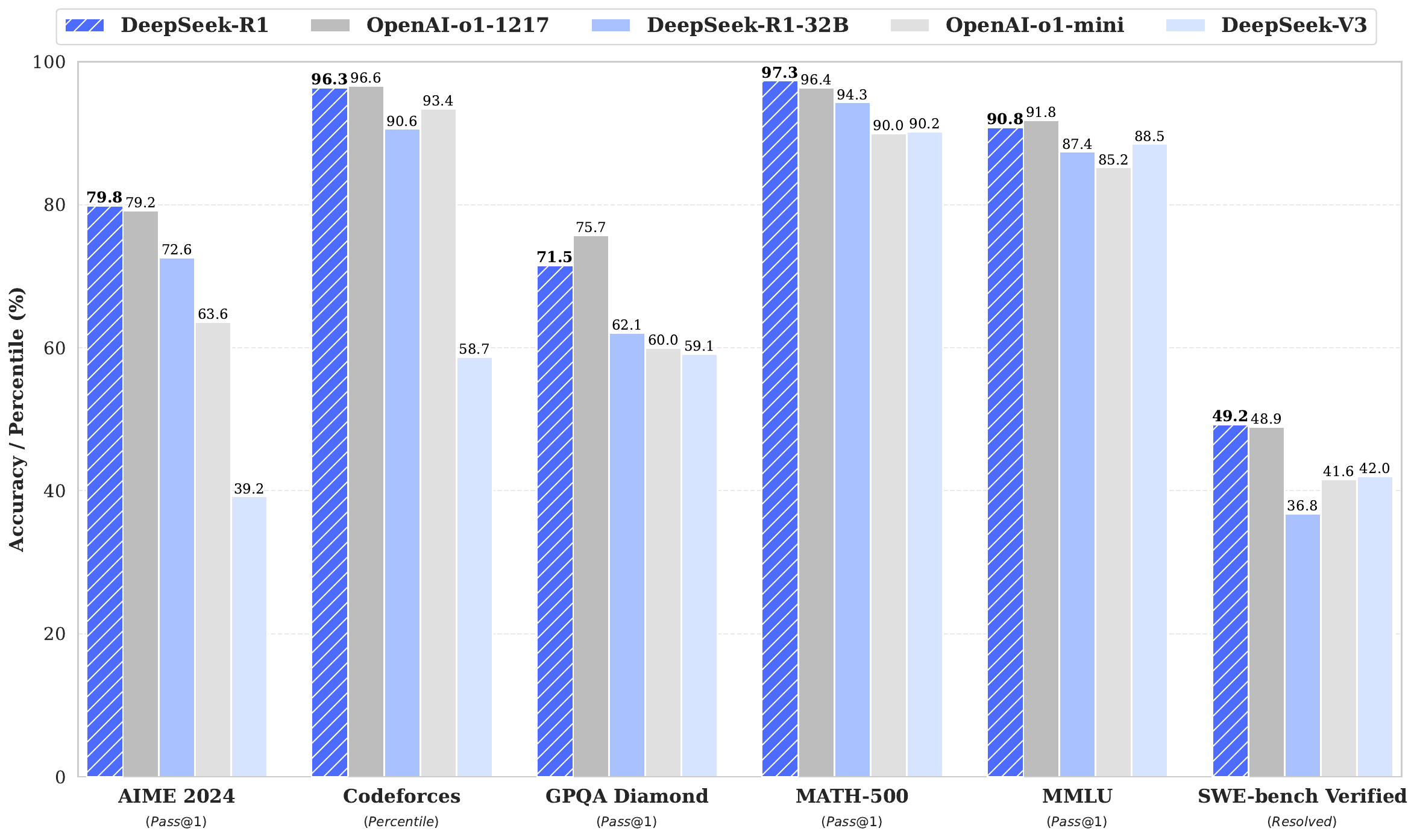
Direct distillation > RL on small models
14B beats QwQ-32B-Preview (55.5% vs 50.0% AIME)
Reasoning patterns transfer effectively across model sizes

Cognitive Behaviors for Self-Improvement

Core question: Why do some models improve with RL while others plateau?

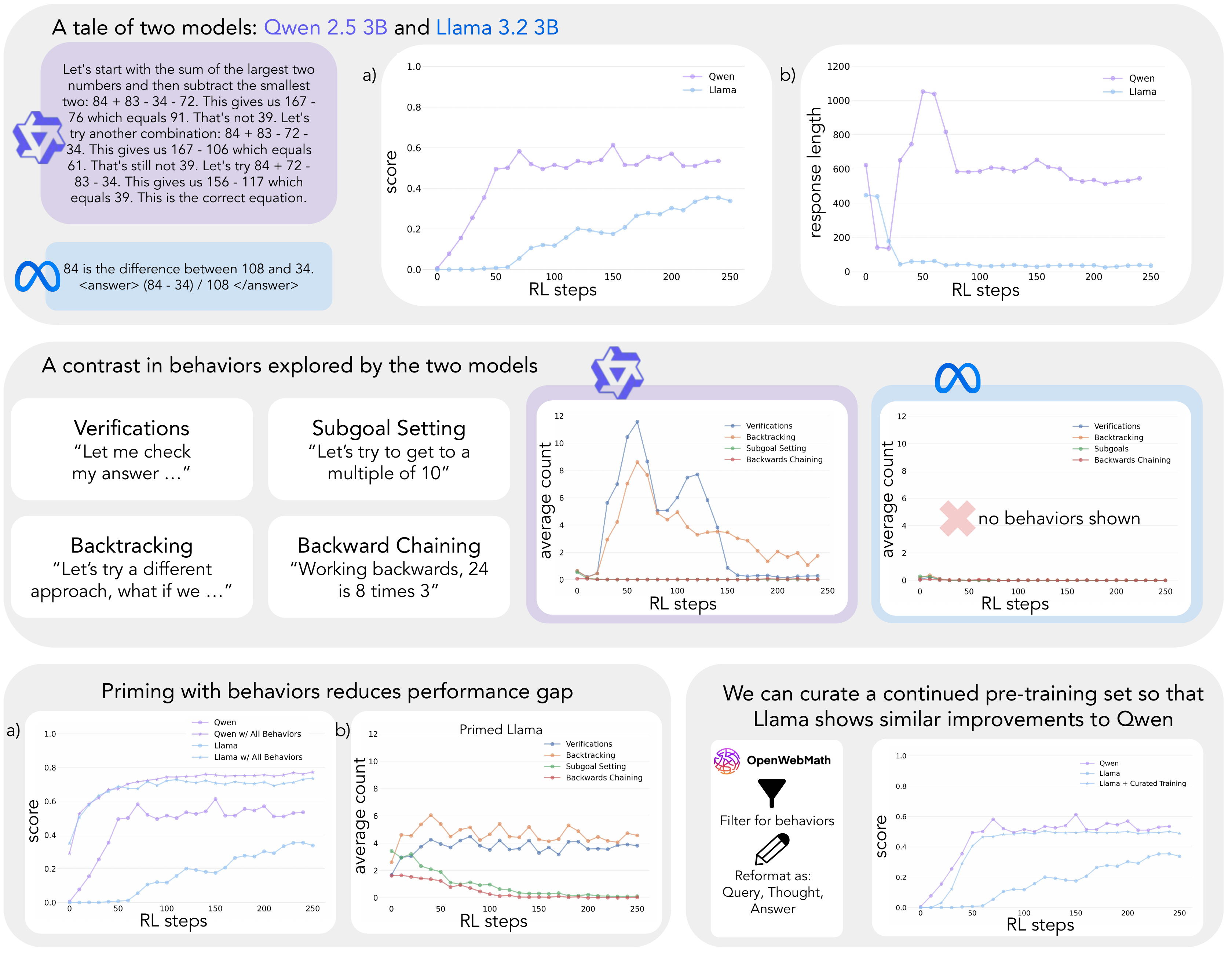
Four critical reasoning behaviors

Verification: Checking intermediate results
Backtracking: Revising approaches when errors detected
Subgoal setting: Breaking problems into steps
Backward chaining: Working backwards from goals

Cognitive Behaviors: Four Key Behaviors

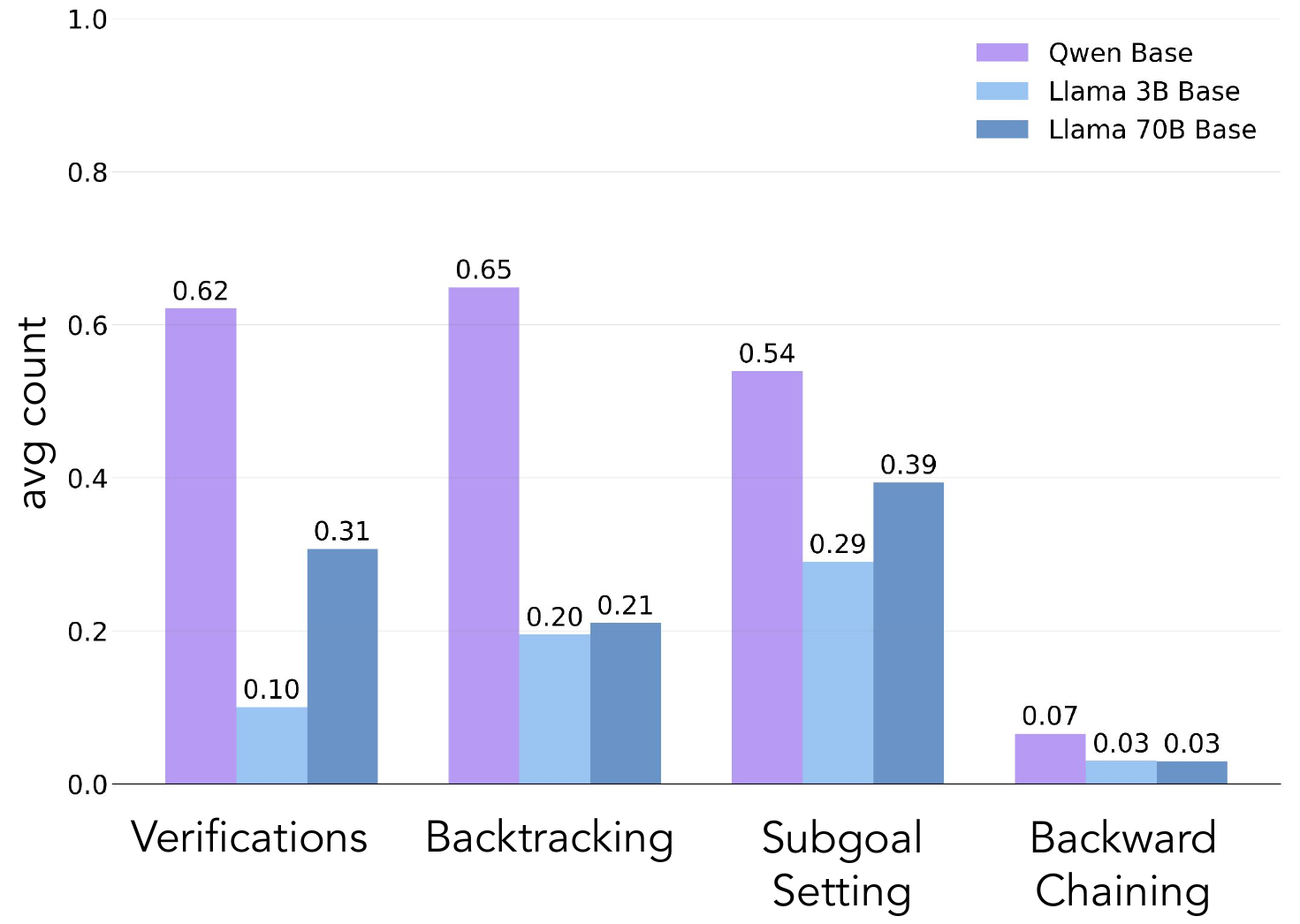
Qwen naturally exhibits these; Llama initially lacks them

Cognitive Behaviors: Priming Results

Priming enables improvement: Llama matches Qwen when primed with reasoning behaviors

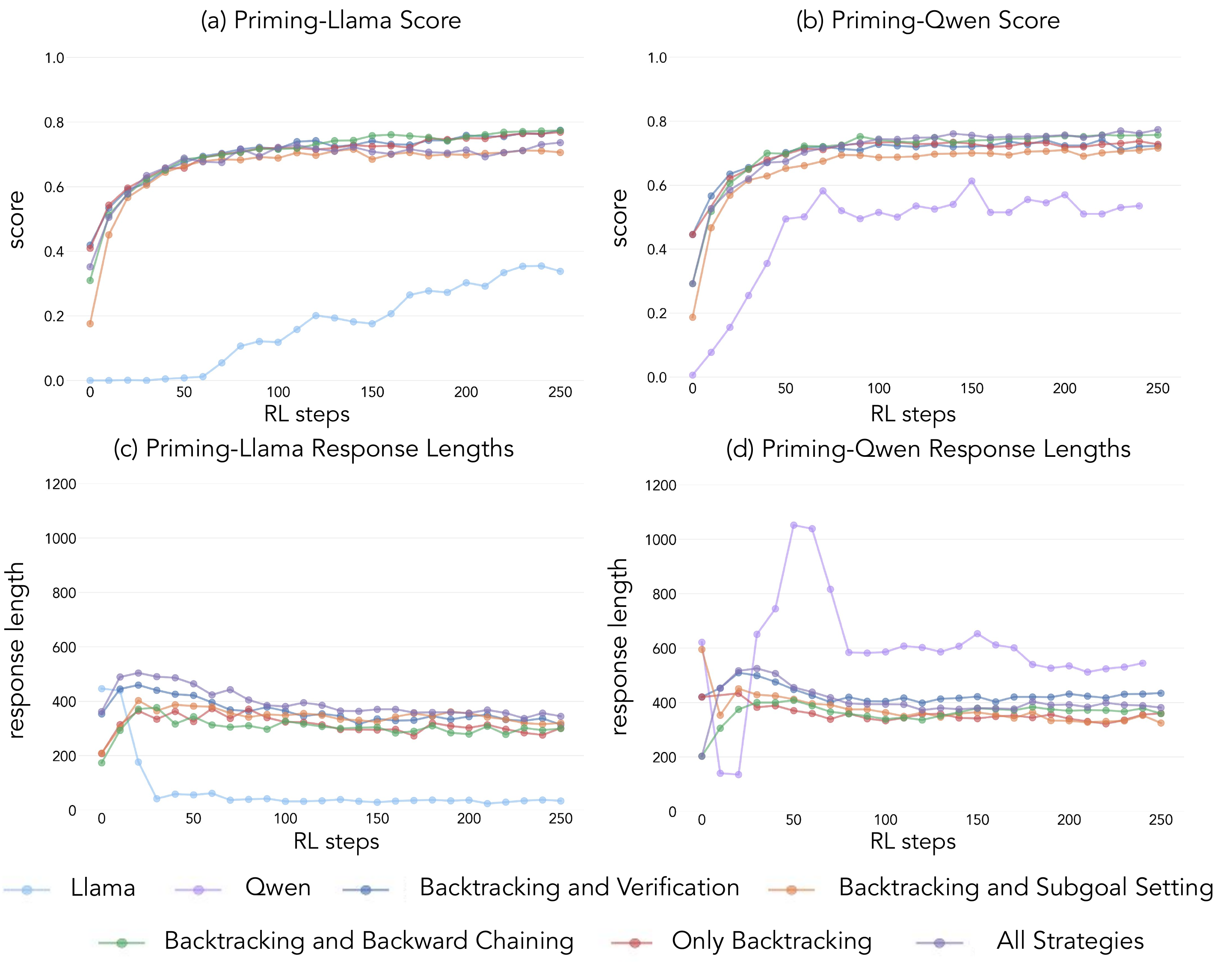
Demystifying Long CoT: Questions

When do long chains-of-thought emerge?
What conditions enable reasoning?
How does training affect CoT length?

Demystifying: Experimental Setting

Supervised fine-tuning (SFT) vs Reinforcement Learning (RL)
Various reward functions and training setups
Length analysis across training iterations
Multiple model sizes and datasets

Demystifying: Long vs Short Results

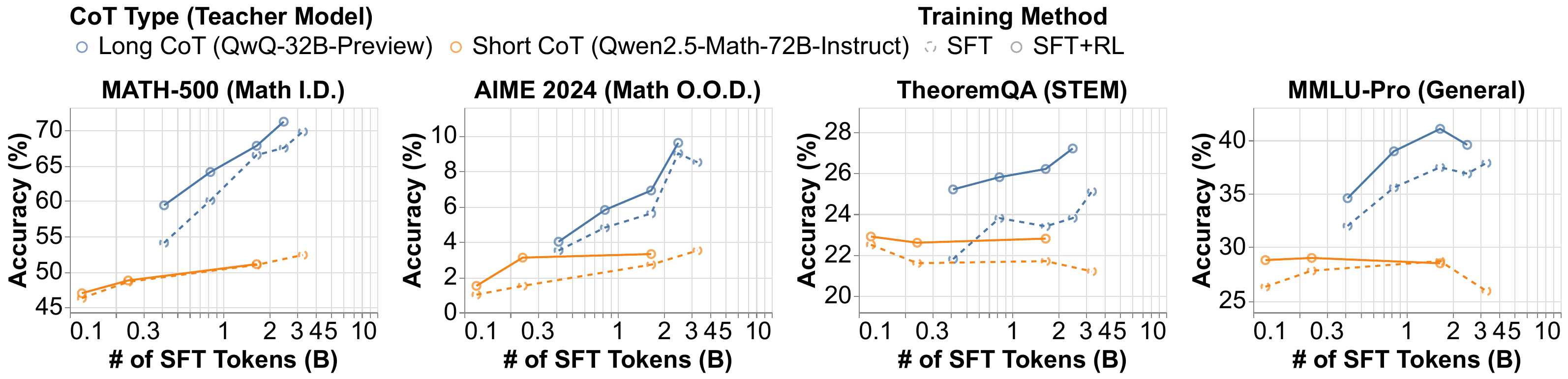
Long CoT SFT scales to higher performance (>70% vs <55%)
Short CoT saturates early with diminishing returns
RL further improves long CoT models significantly

Demystifying: Problems with Length

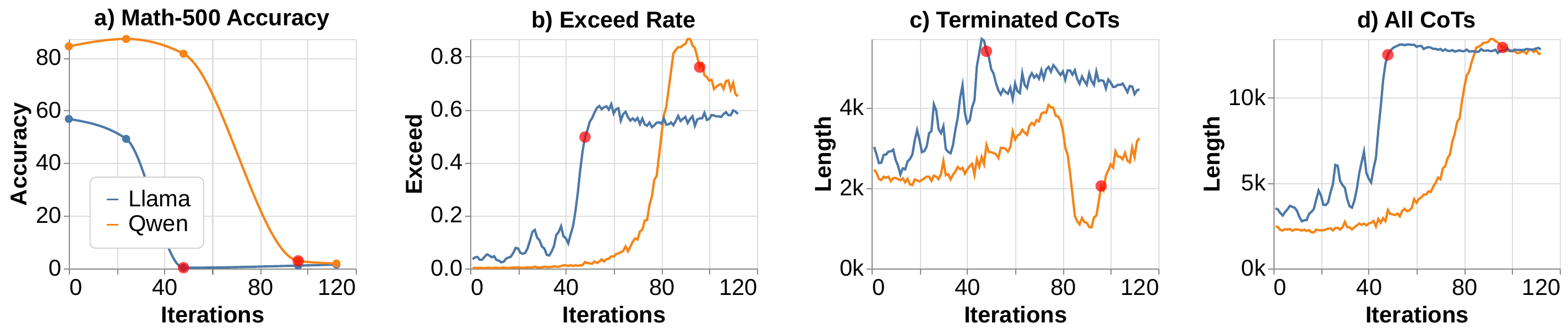
CoT length can exceed context window during training
Causes accuracy drops when responses are truncated

Demystifying: Cosine Reward

Cosine reward to stabilize length

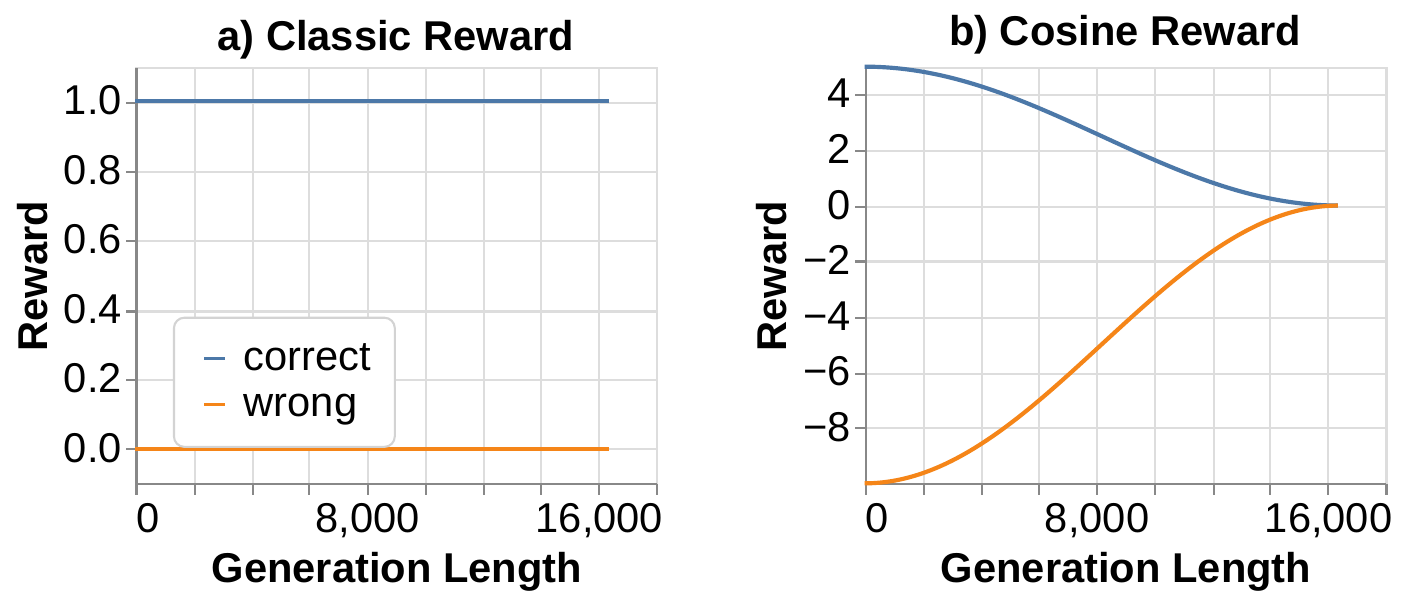
Results

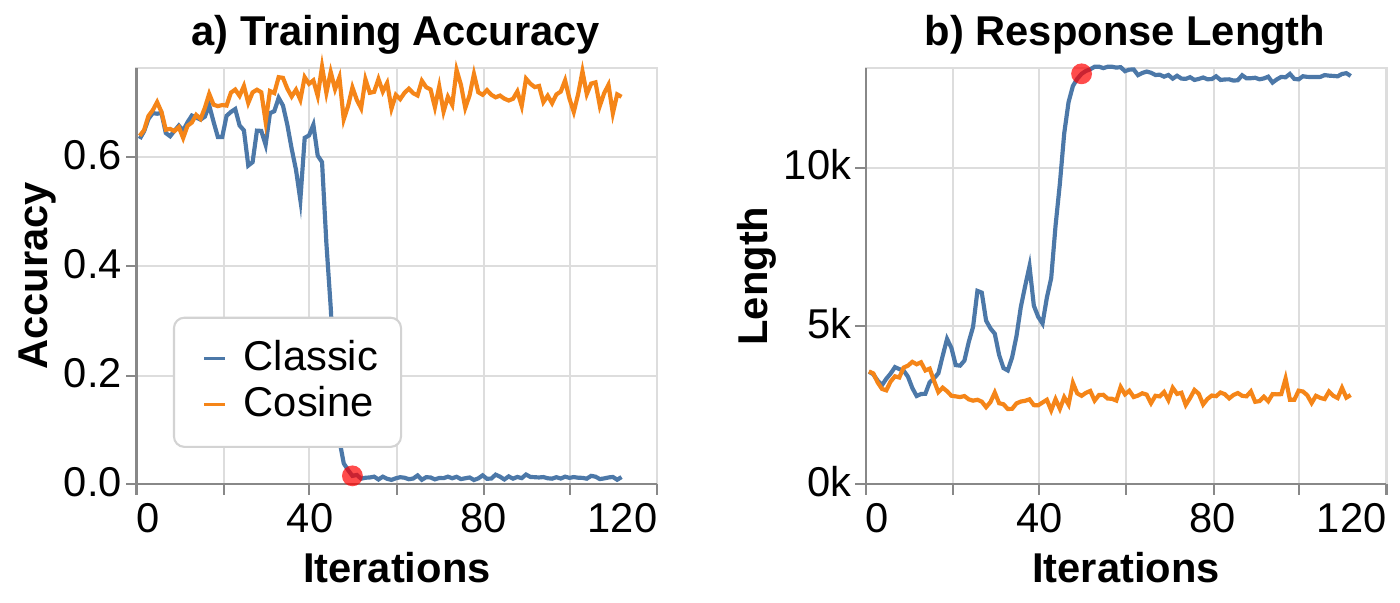
Demystifying: Emergence Conditions

Model capacity: 7B models struggle to develop complex abilities when incentivized
Reward design: Cosine reward prevents length explosion and stabilizes training
Base model quality: Overexposure to short instruction data hinders long CoT development
Training approach: RL from long CoT SFT outperforms RL from base model
Verification: Rule-based verifiers work better than model-based on filtered data

Key insight: Emergence requires careful alignment of multiple factors

SimpleRL-Zoo: Overall Idea

10 different models: LLama3-8B, Mistral-7B/24B, DeepSeek-Math-7B, Qwen2.5 (0.5B-32B)
Zero training: Direct RL from base models (no SFT)
Key question: Can smaller, diverse models exhibit emergent reasoning?
Simple recipe: GSM8K + MATH datasets only

SimpleRL-Zoo: Results on Various LMs

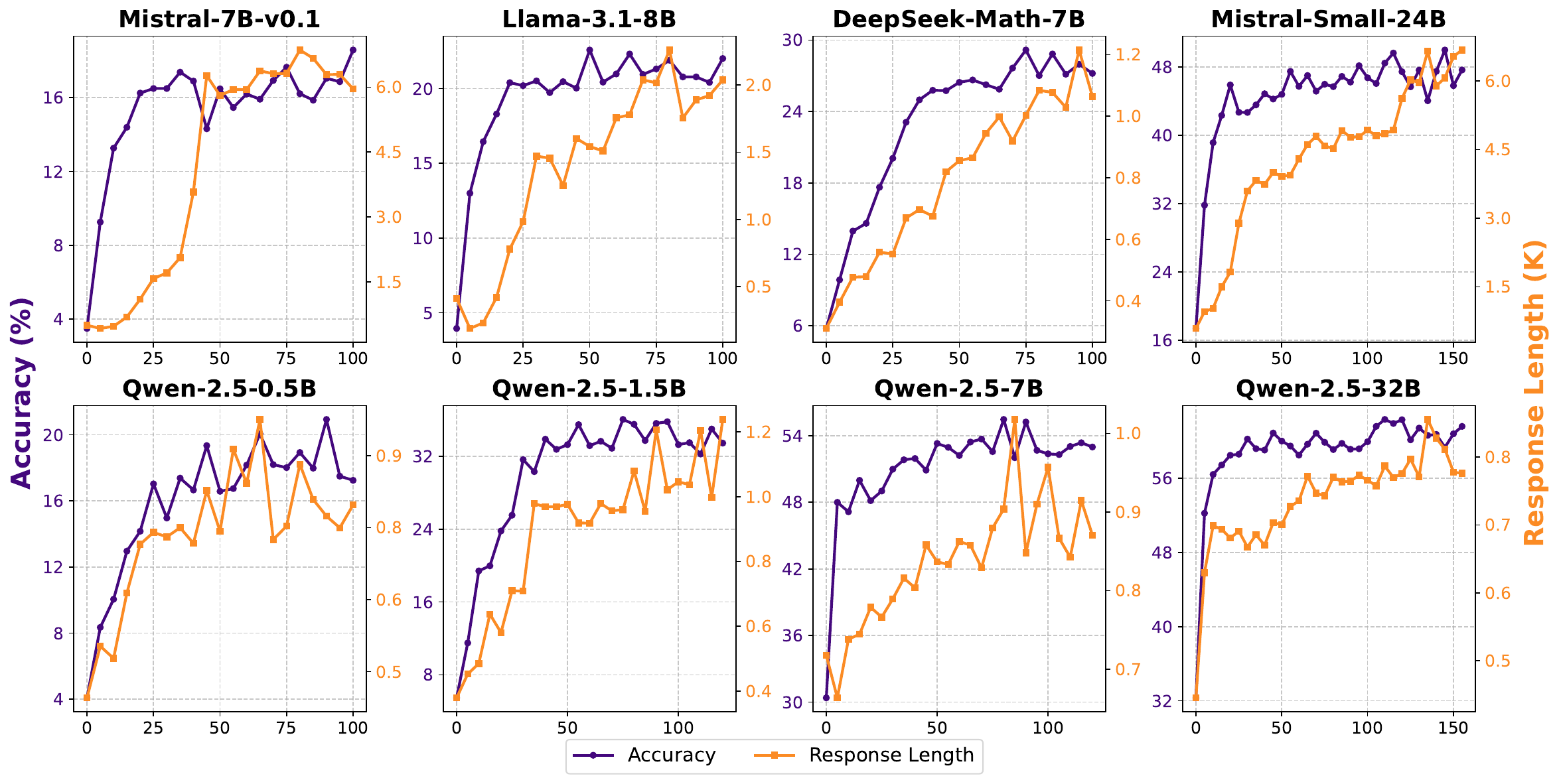
Substantial improvements in accuracy and response length across most models
“Aha moment” observed for first time in small non-Qwen models
Length ≠ reasoning: Increased length doesn’t always correlate with verification behaviors

SimpleRL-Zoo: Discussion of Results

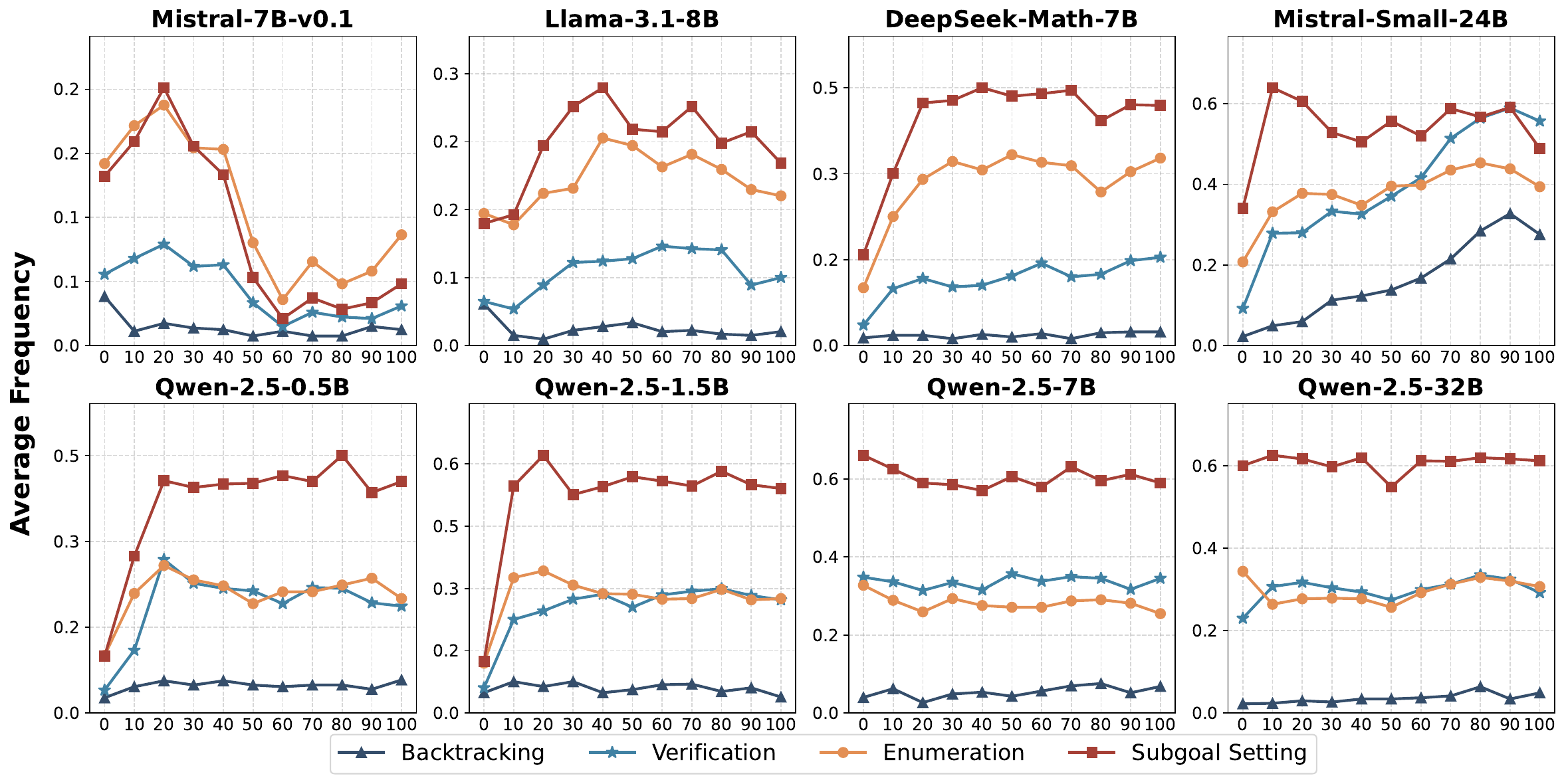
Model-specific patterns: Mistral vs Qwen exhibit opposite behaviors with data difficulty
Training collapse: High difficulty data can break training for some models
SFT harmful: Traditional SFT limits reasoning emergence
Data alignment crucial: Training data must match model’s inherent capabilities

Reasoning Transfer: Main Question

Do improved math reasoning abilities transfer to general LLM capabilities?

Key question: Do gains in solving math problems transfer to:

Other reasoning domains (scientific QA, coding, agent planning)
Non-reasoning tasks (conversation, instruction following)

Motivation: Math has become the poster child of LLM progress, but real-world tasks extend far beyond math

Reasoning Transfer: Experimental Setup

Controlled experiment on Qwen3-14B:

Training data: Math-only (MATH + DeepScaler datasets)
Two paradigms: SFT vs RL (GRPO)
SFT setup: Rejection sampling with Qwen3-32B teacher
RL setup: Answer correctness as reward

Evaluation: 20+ open-weight reasoning models across diverse tasks

Reasoning Transfer: Main Results

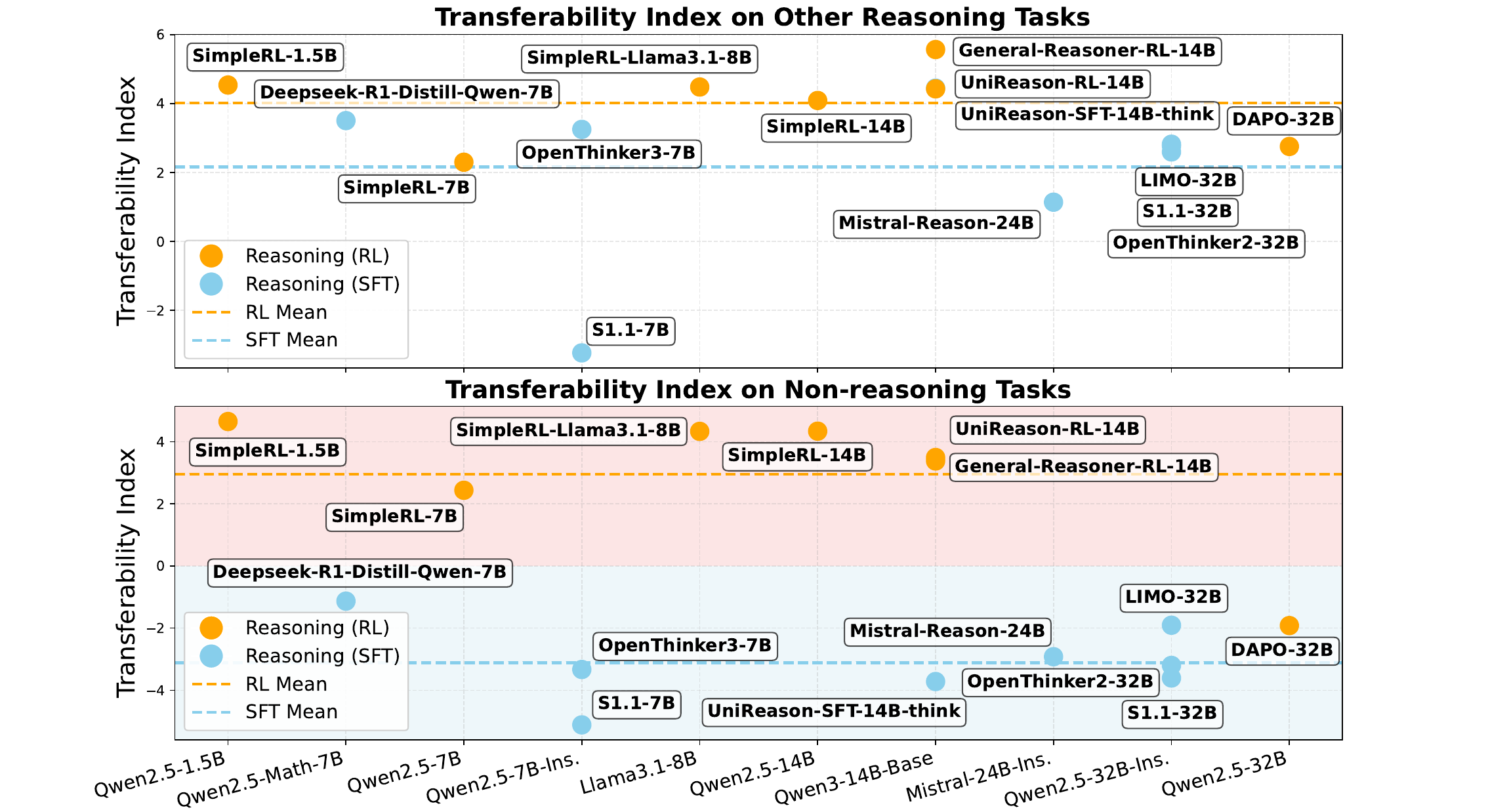
RL models consistently outperform SFT models in transferability across all model sizes and architectures

Reasoning Transfer: What Words Change in Probability

Analysis: SFT induces significant drift in token distributions, while RL preserves general-domain structure

S1: Simple Test-Time Scaling

Minimal data: Only 1,000 carefully curated reasoning samples
Budget forcing: Control thinking duration at test time
Extend thinking: Append “Wait” tokens to encourage more exploration
No RL needed: Just supervised fine-tuning on Qwen2.5-32B

S1: Results Summary

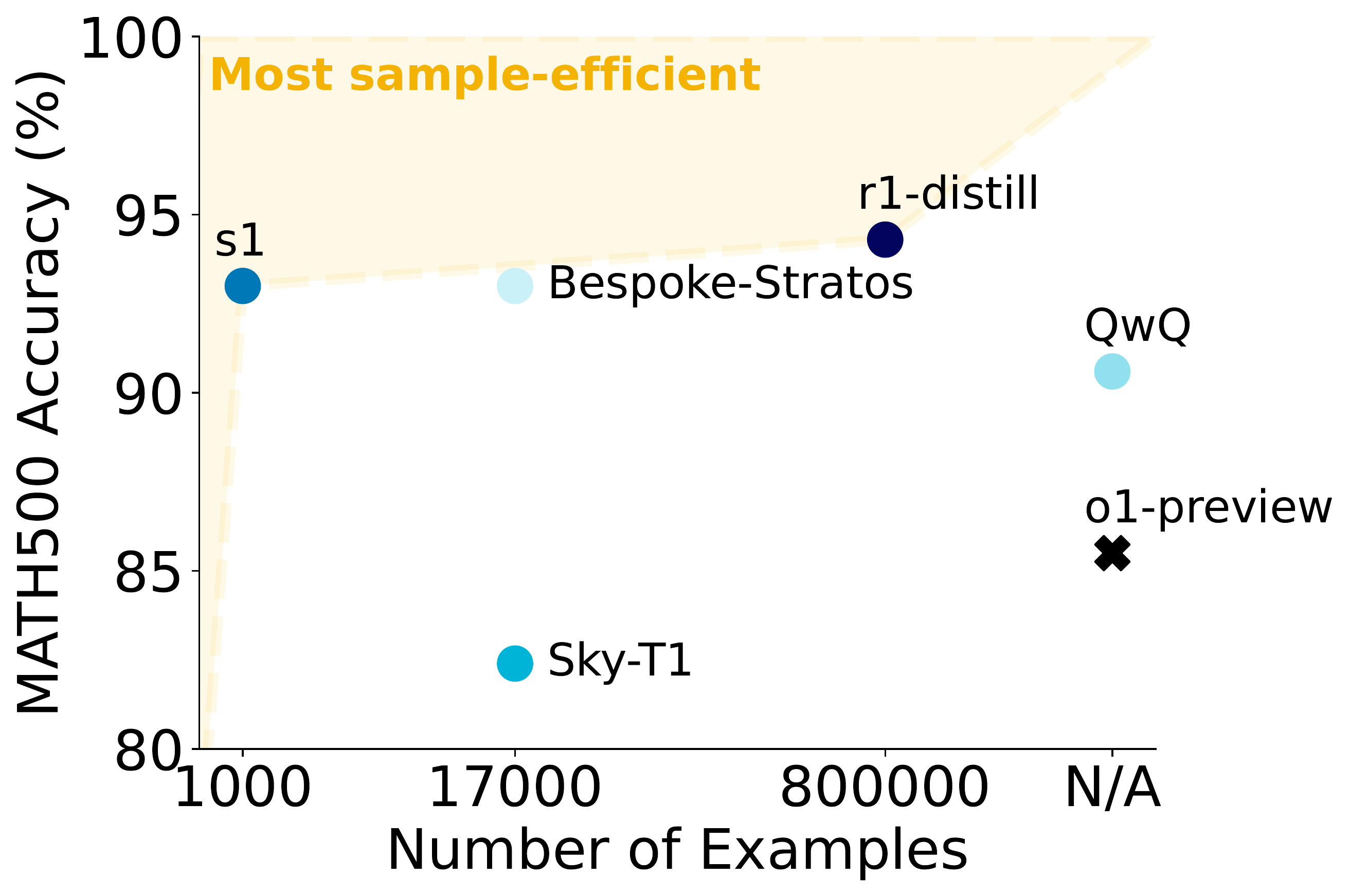
Performance highlights:

MATH: 90.0% vs o1-preview’s 85.5% (+4.5%)
AIME24: 57% vs o1-preview’s 44% (+13%)
Training efficiency: 26 minutes on 16 H100s vs months for competitors

L1: Length Controlled Policy Optimization

Core idea: Control reasoning length with simple prompts like “Think for N tokens”

Key insight: Explicit length control improves reasoning quality and efficiency

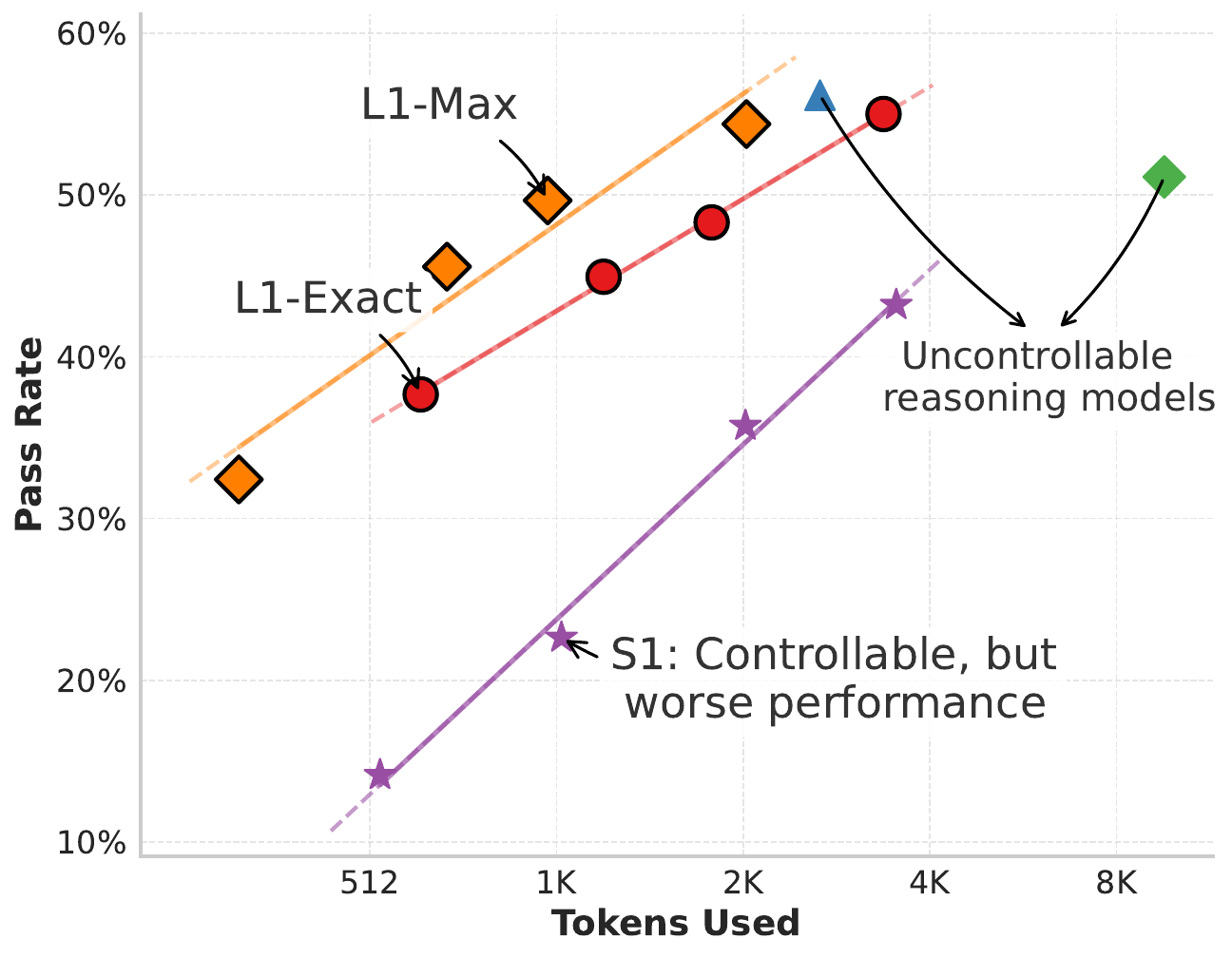
L1: Length Controlled Policy Optimization (LCPO)

Prompt augmentation: “Think for \(n_{gold}\) tokens”
Dual reward: Correctness + length adherence with \(\alpha\) to balance accuracy vs length

\[r(y, y_{gold}, n_{gold}) = \mathbb{I}(y = y_{gold}) - \alpha \cdot |n_{gold} - n_y|\]

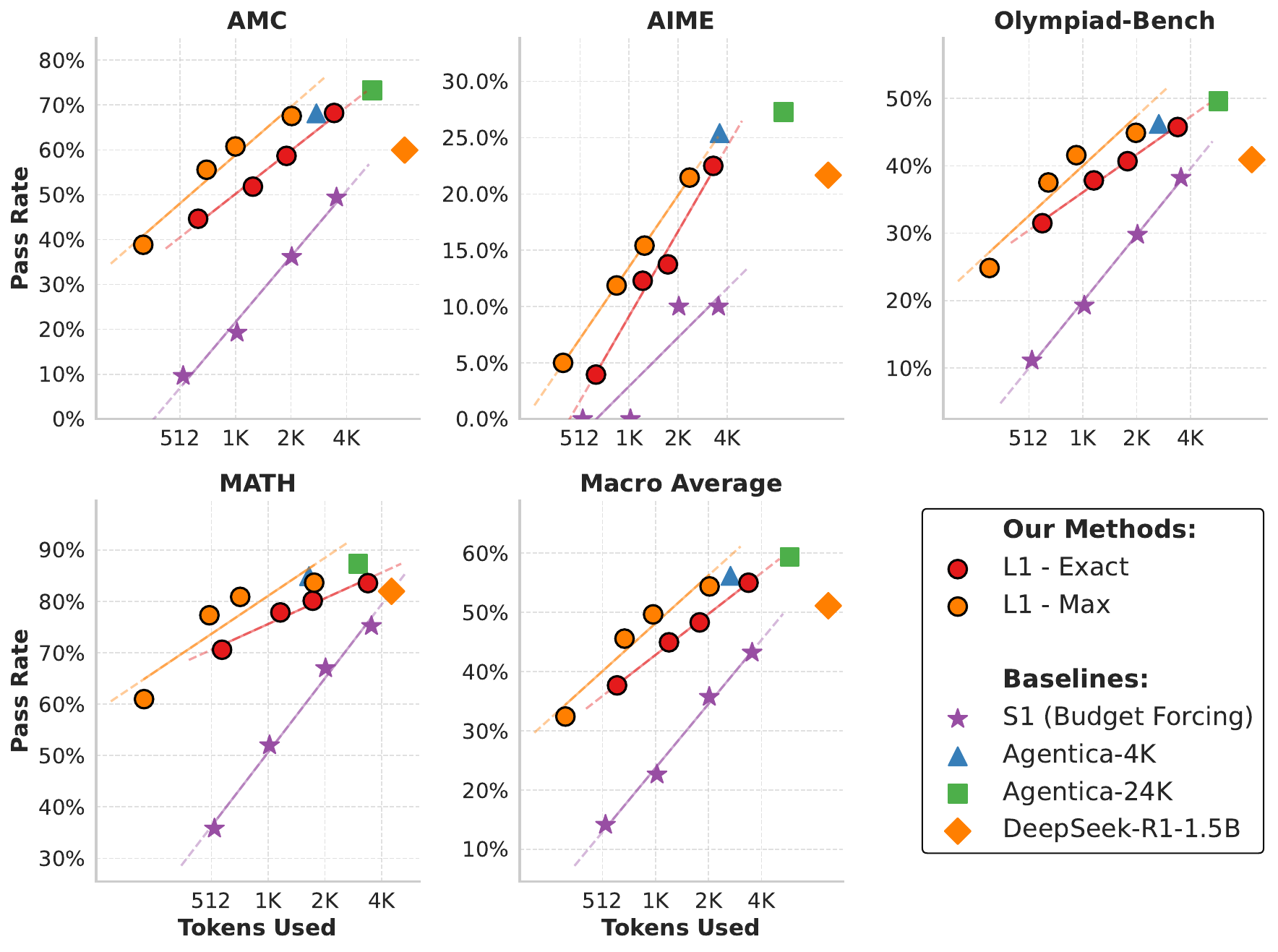
L1: Results

Stream of Search: Main Concept

Stream of Search: Represent search process as flattened language strings

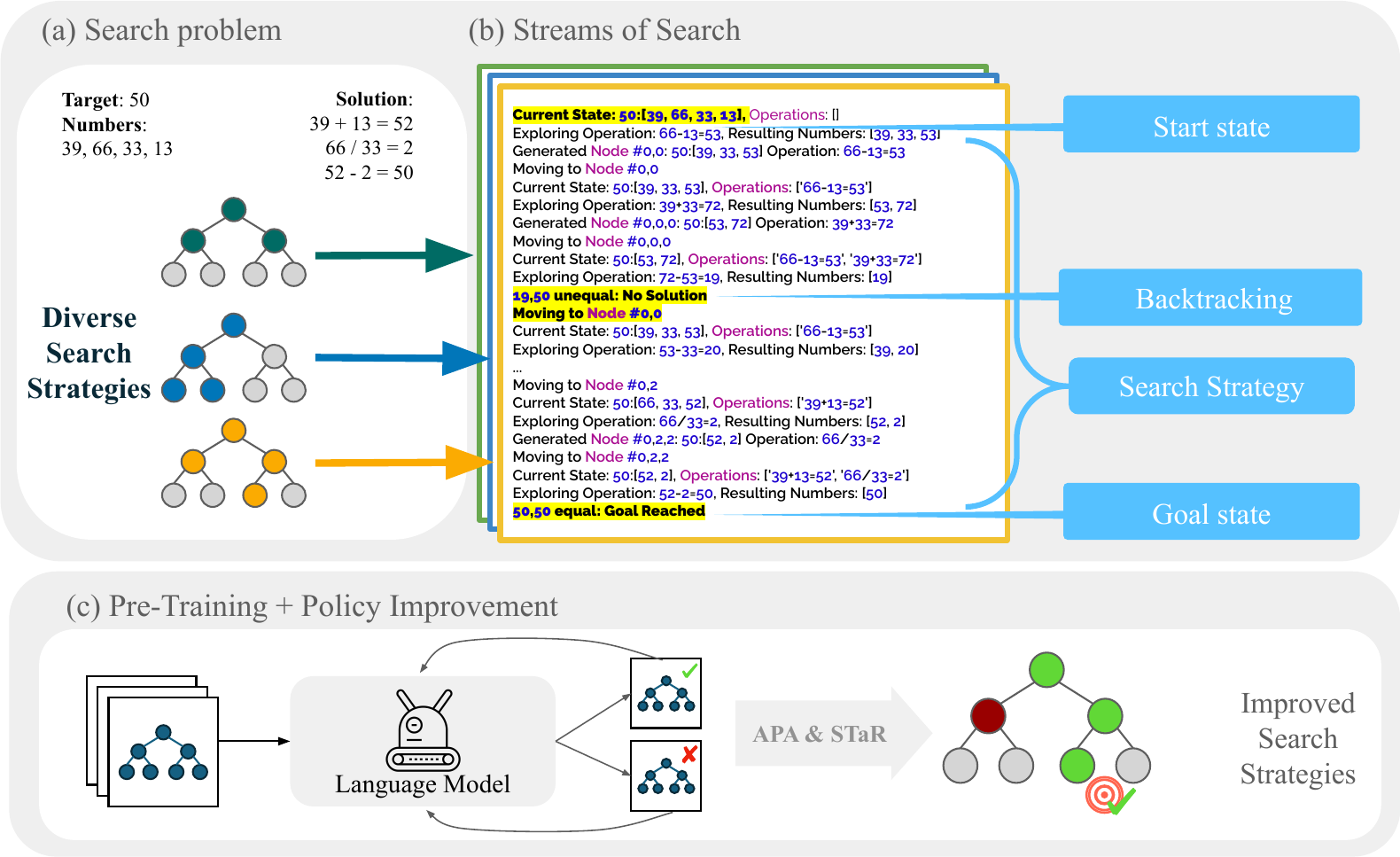
Stream of Search: Method Details

12 diverse search strategies (BFS/DFS variants)
500K search trajectories on Countdown game
Heuristic guidance: Distance to target, factor proximity

Stream of Search: Results

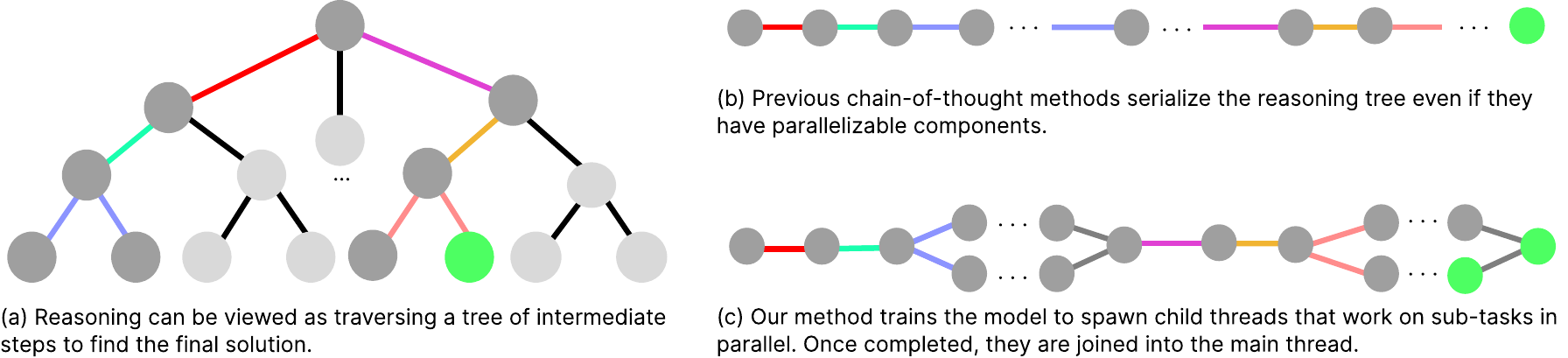
Adaptive Parallel Search

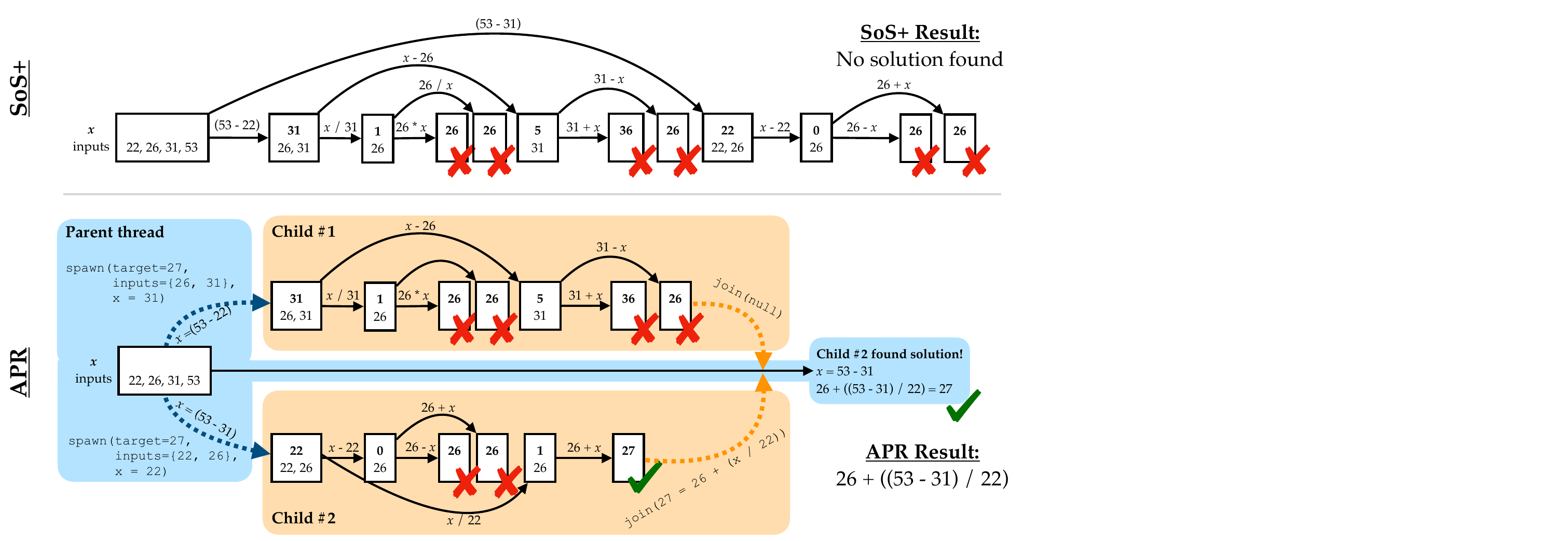
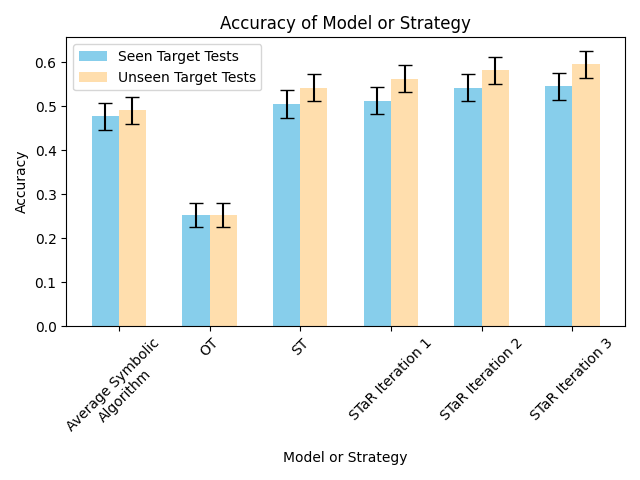
Adaptive Parallel Search: Method Details

spawn(msgs): Create parallel child threads
join(msg): Return results to parent thread
End-to-end RL optimization of parent-child coordination

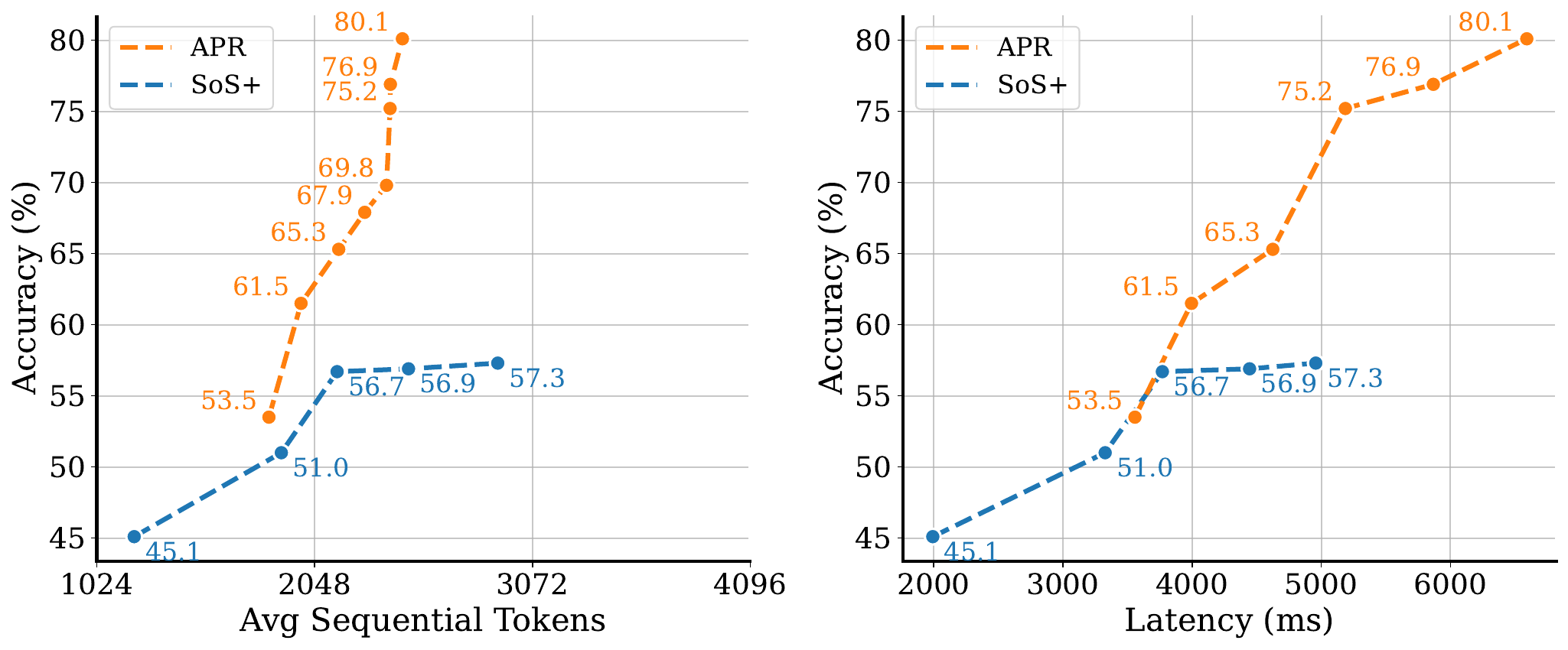
Adaptive Parallel Search: Results

Summary

Key themes in reasoning models:

Training methods: STaR, RL, distillation
Emergence conditions: Compute, data, rewards
Control mechanisms: Length, compute, search
Transfer: Cross-domain reasoning capabilities
Scaling: Larger models, more compute, better performance

Future directions: Better understanding, more efficient methods, broader applications